L'axiome le plus court possible pour la logique booléenne
Les opérateurs de la logique booléenne peuvent être exprimés en termes d'un seul opérateur, NAND ou NOR. En 1913, Henry Sheffer a formulé trois axiomes prouvant que l'algèbre de Boole peut être définie avec un seul opérateur (NAND ou NOR). En 2000, Stephen Wolfram a trouvé un axiome unique pour l'opérateur unique, à partir duquel les axiomes de Sheffer peuvent être prouvés. Wolfram a également montré que c'est l'axiome le plus court possible à partir duquel la logique booléenne peut être construite. En savoir plus dans ce blog.
Obtenez les trois axiomes de Sheffer pour un opérateur représenté par CenterDot, en utilisant les variables formelles a, b, c pour représenter des propositions arbitraires.
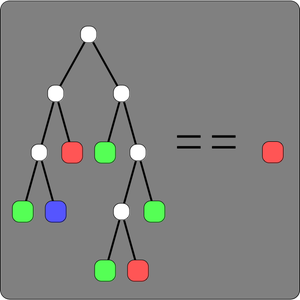
C'est l'axiome le plus court possible pour la logique booléenne, tel que donné par Wolfram.
La fonction FindEquationalProof peut construire les preuves des axiomes de Sheffer à partir de l'axiome de Wolfram.
Il est également possible de prouver l'axiome de Wolfram à partir des axiomes de Sheffer, en démontrant l'équivalence des deux systèmes d'axiomes.
D'autres propriétés du NAND, comme la commutativité, peuvent également être déduites.