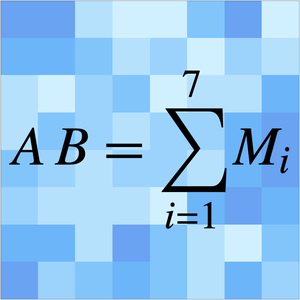Compare Algorithms Using Asymptotic Relations
In computational complexity, algorithms are classified by their behavior for large inputs, typically taken to be at infinity. Two algorithms are compared by whether the runtime of one is AsymptoticLessEqual (big 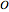 ), AsymptoticLess (little
), AsymptoticLess (little 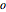 ), AsymptoticGreaterEqual (big
), AsymptoticGreaterEqual (big 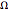 ) or AsymptoticGreater (little
) or AsymptoticGreater (little 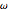 ) the other's runtime.
) the other's runtime.
The traveling salesperson problem (TSP) consists of finding the shortest route connecting  cities. A naive algorithm is to try all
cities. A naive algorithm is to try all 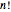 routes. The Held–Karp algorithm improves that to roughly
routes. The Held–Karp algorithm improves that to roughly 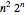 steps. Show that
steps. Show that 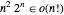 and hence the Held–Karp algorithm is faster.
and hence the Held–Karp algorithm is faster.
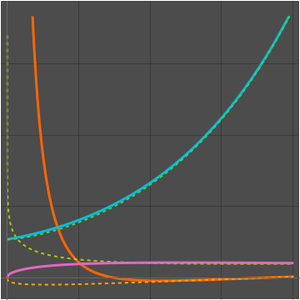
Both algorithms show that the complexity class of TSP is no worse than EXPTIME, which are problems that can be solved in time 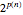 . For example,
. For example, 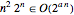 for any
for any 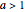 , so the Held–Karp algorithm has exponential runtime.
, so the Held–Karp algorithm has exponential runtime.
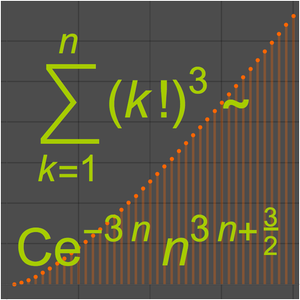
For the factorial function, a linear exponential does not suffice because 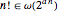 .
.
However, the factorial still has exponential runtime because 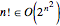 .
.
Approximate solutions can be found in 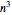 time, so the approximate TSP is in the complexity class P of problems solvable in polynomial time. Any polynomial algorithm is faster than an exponential one, or
time, so the approximate TSP is in the complexity class P of problems solvable in polynomial time. Any polynomial algorithm is faster than an exponential one, or 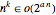 .
.