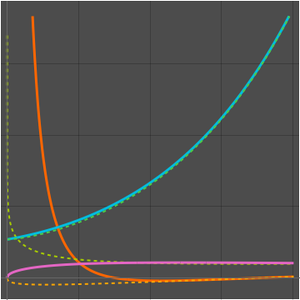
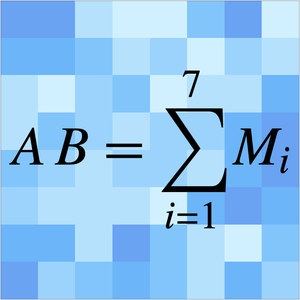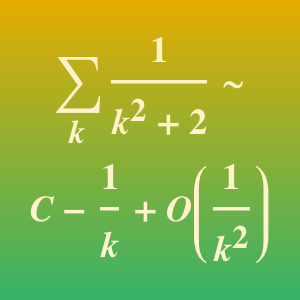用渐近关系比较算法
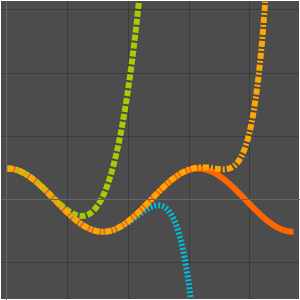
在计算复杂度方面，根据对较大输入（通常为无穷大）的行为对算法进行分类。通过运算时间之间的关系，是 AsymptoticLessEqual (big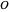 
)、AsymptoticLess (little 
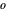)、AsymptoticGreaterEqual (big 
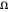) 或 AsymptoticGreater (little 
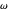) 来比较两种算法。
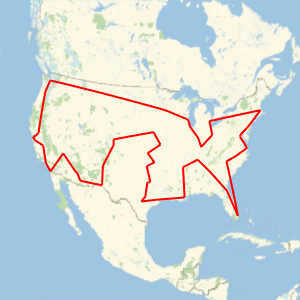
旅行推销员问题 (TSP) 要求找到连接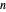 
个城市的最短路径。一个简单直接的算法是尝试所有 
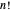条路线。Held–Karp 算法将其改进为大约需要 
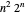步。证明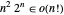 
，因此 Held–Karp 算法要更快。
两种算法都显示 TSP 的复杂等级不比 EXPTIME 更高，EXPTIME 问题的求解时间为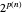 
。例如，对于 
，
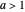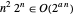，因此 Held–Karp 算法的计算时间为指数级。
对于阶乘函数，线性指数是不够的，因为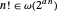 
。
但是，阶乘的计算时间依然为指数级，因为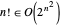 
。
可在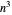 
时间内求得近似解，因此，近似 TSP 的复杂性级别为 P 级，可在多项式时间内求解。任何多项式算法都比指数算法快，或 
。
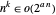