Approximate the Sequence of Involution Counts (AsymptoticRSolveValue)

An involution is a permutation that is its own inverse. In the following example, the difference equation for the sequence of the number of involutions acting on elements is obtained using FindSequenceFunction. An asymptotic approximation is then computed by using an inexact initial value at in AsymptoticRSolveValue. The resulting hybrid symbolic-numeric formula gives an excellent approximation for the 1000 ^th term of the sequence.

Define a function testing if a permutation is its own inverse and is thus an involution.

Compute the number of involutions on elements for from 1 to 10.

Use FindSequenceFunction to obtain the recurrence relation for the sequence.

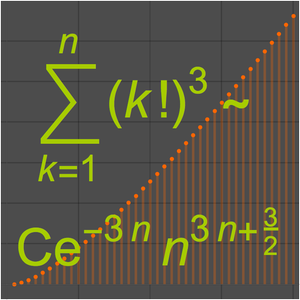
Obtain the leading terms in the asymptotic expansion.

Compare the approximate and actual values.