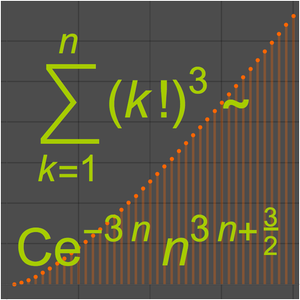
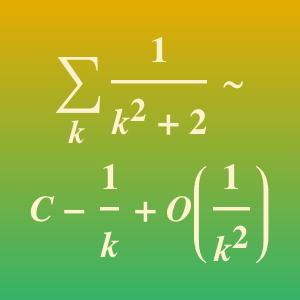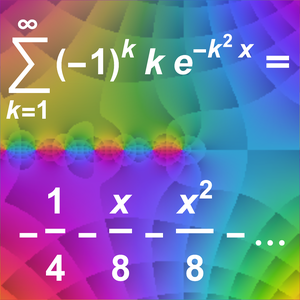Verify Asymptotic Approximations

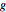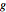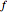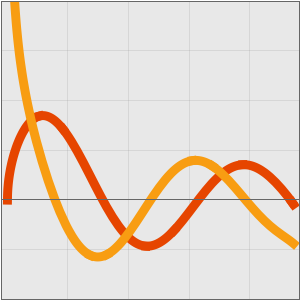
If a function approximates a function with a relative error that vanishes as one approaches the base point, then is said to be AsymptoticEquivalent to , often written as 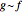. A classic example is Stirling's approximation to the factorial function.

Since the relative error goes to zero, the ratio of the functions goes to .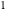

Stirling's approximation is striking because while the relative error goes to zero, the absolute error goes to infinity.

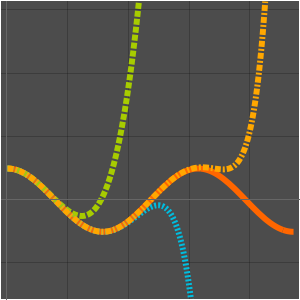
Taylor series give asymptotic approximations.

Laurent series also give asymptotic approximations.

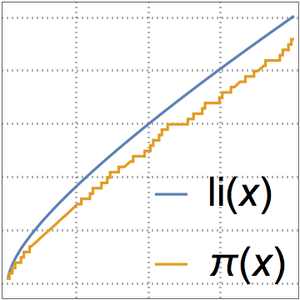
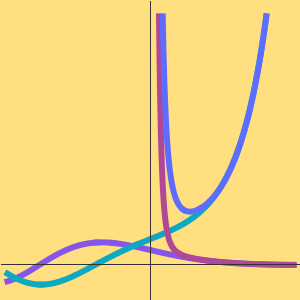
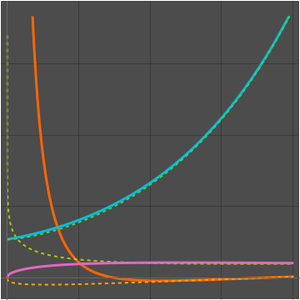
The prime number theorem states that 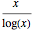is an asymptotic approximation to the prime-counting function .

A better approximation is given by the logarithmic integral function .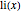

Compare the prime-counting function and the two approximations.