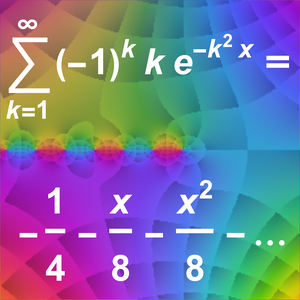Explore a Divergent Asymptotic Expansion (AsymptoticIntegrate)
Asymptotic expansions are often given in terms of divergent series. Typically, the first few terms of the divergent series provide an excellent approximation for the problem, but the quality of the approximation deteriorates with the addition of further terms in the series. This phenomenon is illustrated in the following example of a definite integral depending on a parameter.
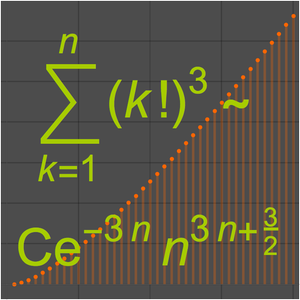
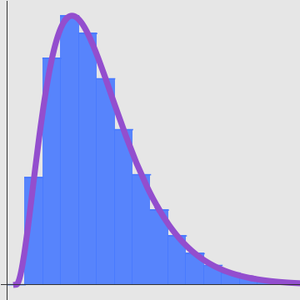
Consider the following series expansion for a definite integral.
The series diverges for all nonzero values of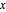 
.
While the series is classically divergent, it provides an excellent asymptotic approximation for the integral. For example, the following numerical comparison shows that the approximation is fairly accurate.
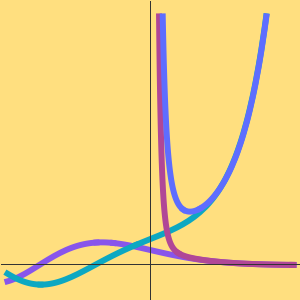
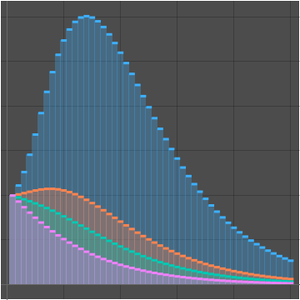
The approximation is no longer accurate with a larger number of terms, which is typical behavior for an asymptotic series.
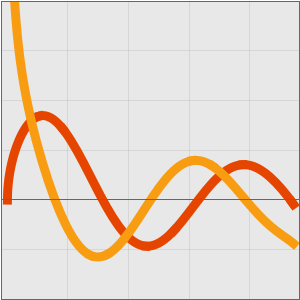
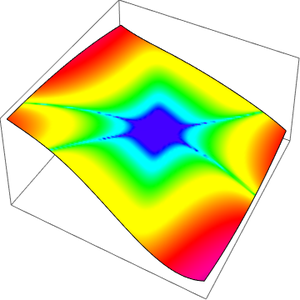
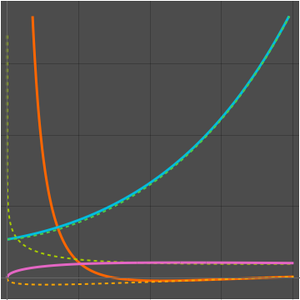
The following plot shows that, for a fixed value of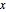 
, the asymptotic series provides a good approximation when the number of terms lies within a certain range (depending on 
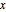). The approximation begins to diverge when the number of terms is increased beyond this range.
Obtain the exact result using Integrate or using Regularization.
