Highlight Features with Shading
Different color schemes can be used to highlight features of a complex function.
Define a complex function 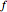 with a pole at
with a pole at 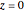 and zeros at
and zeros at 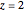 ,
,  and
and  .
.
By default, zeros of the complex function 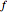 are bright and the colors fade to white for large values of
are bright and the colors fade to white for large values of 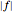 relative to the rest of the plot.
relative to the rest of the plot.
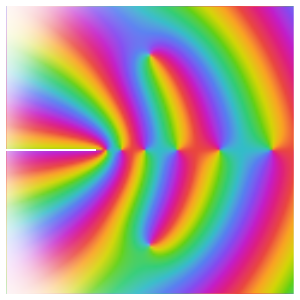
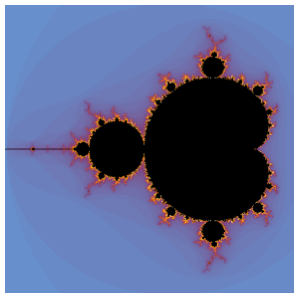
Emphasize the zeros by using a globally scaled color function that is black at zeros and white at poles.
Using a locally scaled color function keeps more of the intermediate colors and has better contrast with the black zeros and white poles.
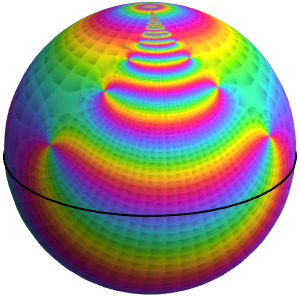
Cyclically darkening the colors based on 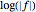 creates bands and makes it easy to see values that have the same magnitude, even when the function spans a large range of values.
creates bands and makes it easy to see values that have the same magnitude, even when the function spans a large range of values.
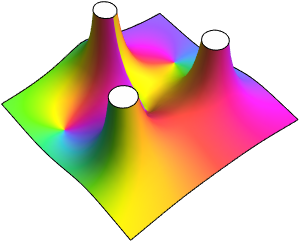
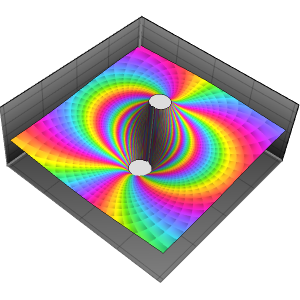
Shade using a color function such that each zero has a small color wheel around it and each pole is surrounded by an accumulation of contours of 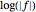 .
.
Cyclically darkening the colors using 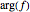 creates bands that make it easy to see values that have the same argument.
creates bands that make it easy to see values that have the same argument.
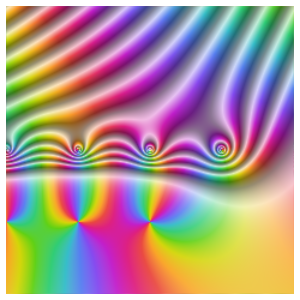
Darkening the colors based on both 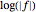 and
and 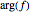 highlights where the magnitude and arguments are the same.
highlights where the magnitude and arguments are the same.
Darken to give the appearance of curves of constant 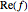 and
and 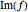 and lighten to give the appearance of curves of constant magnitude.
and lighten to give the appearance of curves of constant magnitude.