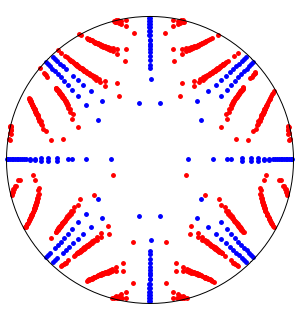
Gerschgorin Disks
The Gerschgorin circle theorem (http://mathworld.wolfram.com/GershgorinCircleTheorem.html) states that every eigenvalue of the square matrix 
is in at least one of the disks whose centers are the diagonal entries of 
and whose radii are a sum of the entries in each row.
Generate a random complex matrix 
.
The diagonal entries of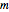 
are the centers of the Gerschgorin disks.
The radius of the 
th Gerschgorin disk, 
, is the sum of the moduli of the entries in row 
, excluding the diagonal entry.
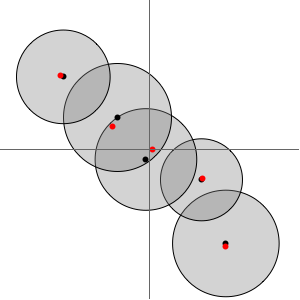
Make the Gerschgorin disks for the matrix.
Show the eigenvalues (red) in the Gerschgorin disks.
