Eigenvalues of a Random Matrix

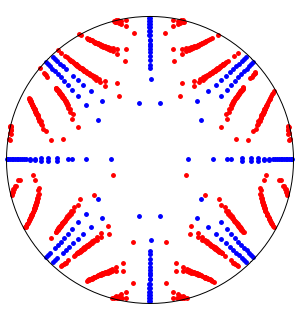
For a random real matrix whose entries are chosen from [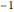,1], the eigenvalues with positive imaginary part are uniformly distributed on the upper half of a disk, and those with negative imaginary part are the complex conjugates of the eigenvalues on the upper half.

The eigenvalues of a random complex matrix are uniformly distributed on a disk since they do not occur in complex conjugate pairs.

Plot an approximation of the distribution of eigenvalues of 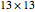Frobenius companion matrices with random integer entries from .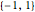