Visualize Eigenvalues of Graphs

Eigenvalues of graphs can give information about the structural properties of the graph.

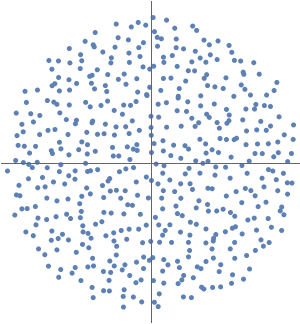
Generate an acyclic directed graph from an initial base graph.

If a graph is acyclic, then its adjacency matrix is nilpotent and all of its eigenvalues are zero.

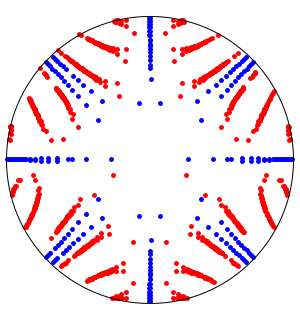
If a graph is symmetric, then its adjacency matrix is symmetric and its eigenvalues are real.

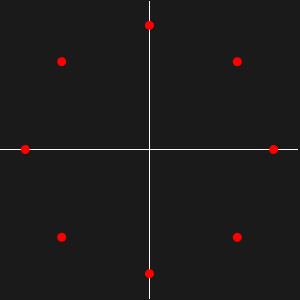
If a graph is bipartite, then the spectrum of its adjacency matrix is rotationally symmetric with respect to 0. That is, if 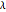is an eigenvalue of the adjacency matrix, then so is .

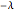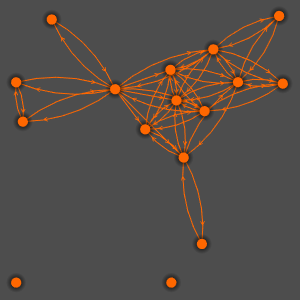
Generate a graph showing a set of symbols that link to one another in the Wolfram documentation.

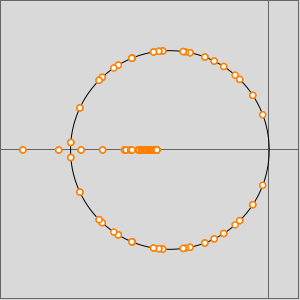
Plotting the eigenvalues of the graph shows that cycles are present, but that the graph is neither symmetric nor bipartite.

The graph is not symmetric because ComplexExpand links to Complex, Conjugate, Im and Re, but not vice versa.