Solutions of Complex ODEs
Solve the complex ordinary differential equation 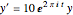 with initial condition
with initial condition 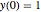 and visualize the behavior.
and visualize the behavior.
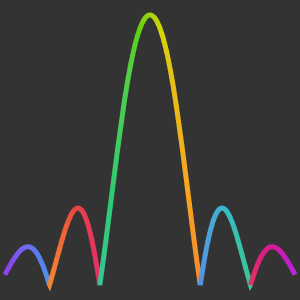
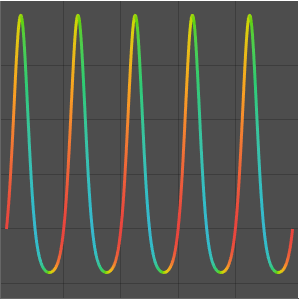
Plot the real and imaginary parts of  as a function of the real variable
as a function of the real variable 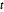 . Both parts are oscillatory, but the imaginary component stays mostly positive, while the real part is symmetric about zero.
. Both parts are oscillatory, but the imaginary component stays mostly positive, while the real part is symmetric about zero.
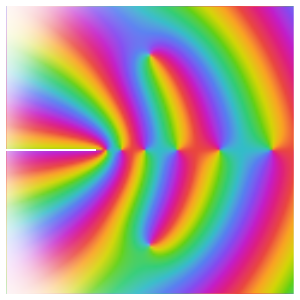
Plot 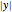 as a function of the real variable
as a function of the real variable  .
.
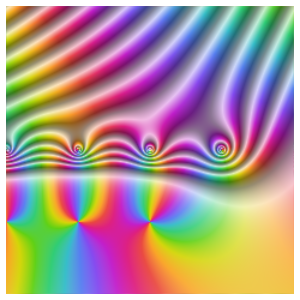
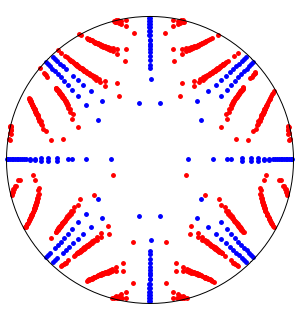
Plot the solution parametrically in the complex plane by sampling at different values of 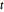 .
.
show complete Wolfram Language input