Strukturelles Optimierungsproblem
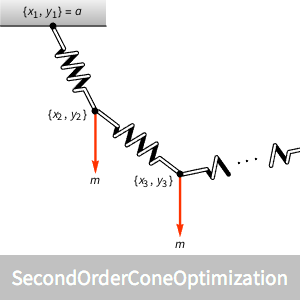
Ermitteln Sie die Form einer Kettenlinie, die aus mehreren Federn besteht, mit einer Masse an jeder Gliederverbindung.
Dieses Beispiel zeigt, wie die Bedingung der kleinstmöglichen potentiellen Energie als Problem der Variationsrechnung mit Kegel-Optimierung 2. Ordnung dargestellt werden kann, das man mit SecondOrderConeOptimization ganz leicht lösen kann.
Ermitteln Sie die Form einer Kettenlinie, die aus 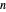 Federgliedern besteht, mit einer Vertikallast am Ende jedes Glieds. Ziel ist es, auf Grundlage der Positionen der Gliedenden
Federgliedern besteht, mit einer Vertikallast am Ende jedes Glieds. Ziel ist es, auf Grundlage der Positionen der Gliedenden 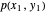 und
und 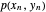 die Gliedpositionen
die Gliedpositionen 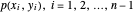 zu finden.
zu finden.
Die potentielle Energie durch die Schwerkraft (ohne Berücksichtigung des Gewichts der Federn) ist 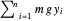 , wobei
, wobei 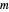 die Vertikallast jedem Ende und
die Vertikallast jedem Ende und 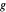 die Standard-Schwerkraft ist.
die Standard-Schwerkraft ist.
Die potentielle Energie aufgrund der Spannung in der Feder durch Dehnung ist 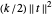 , wobei
, wobei 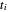 die Dehnung in der Feder
die Dehnung in der Feder 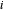 ist und
ist und 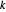 die Steifigkeit der Feder ist. Mit
die Steifigkeit der Feder ist. Mit 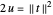 wird die Energie in
wird die Energie in 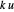 umgewandelt.
umgewandelt.
Eine zusätzliche Einschränkung 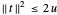 muss aufgrund der Transformation hinzugefügt werden.
muss aufgrund der Transformation hinzugefügt werden.
Die Enden der Gliederkette werden an den Positionen 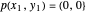 und
und 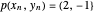 eingespannt.
eingespannt.
Da  konvex ist, genügt es, wenn jede Feder die Bedingung
konvex ist, genügt es, wenn jede Feder die Bedingung 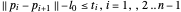 erfüllt, wobei
erfüllt, wobei 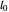 die Länge jeder Feder in Ruhelage ist.
die Länge jeder Feder in Ruhelage ist.
Die Konstruktionsparameter sind folgendermaßen dargestellt:
Die endgültige Zielfunktion ist die Summe aus Schwerkraft und Federpotentialenergie, die minimiert werden muss.
Finden Sie die Endpunkte der einzelnen Federglieder.
Visualisieren Sie die Form der resultierenden Federkette.
Die Dehnung ist am größten für die Glieder in der Nähe der Enden der Gliederkette. Die Verbindungen 11 und 12 haben die geringste Dehnung.
Die Lösung ist schnell genug, um die Anzahl der Links und die Endpunkte zu manipulieren.