Quader mit maximalem Volumen
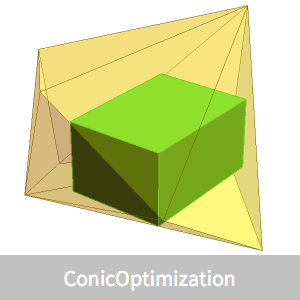
Ermitteln Sie den achsenparallelen Quader mit maximalem Volumen, der in ein konvexes Polyeder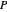 
eingeschrieben ist.
Dieses Beispiel zeigt, wie die Optimierung eines Produkts mit positiven Vorzeichen in Form eines konvexen Kegels ausgedrückt werden kann, und mit ConicOptimization in Optimierungsaufgaben eingesetzt werden kann.
Nehmen Sie ein konvexes Zufallspolyeder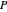 
her, das als konvexe Hülle von Zufallspunkten konstruiert ist.
Ermitteln Sie einen unteren Eckpunkt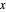 
des Quaders und einen Vektor der Seitenlänge 
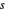, damit Sie den Quader in der Wolfram Language mit 
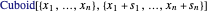darstellen können. Das Volumen des Quaders ist das Produkt seiner Seitenlängen, daher ist es das Ziel, 
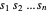zu maximieren. Wenn alle Ecken des Quaders in 
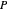liegen, dann sind auch alle Punkte im Quader in 
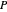. Die Ecken können durch 
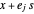ausgedrückt werden, wobei 
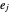in der Menge 
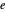aller möglichen n‐Tupel der Elemente von 
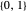liegt.
Das Problem ist das folgende:
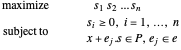
Da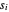 
nichtnegativ ist, ist die Maximierung des Produkts 
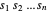dasselbe wie die Maximierung des geometrischen Mittels 
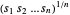, das konkav ist. Das Maximieren von 
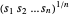ist äquivalent zur Minimierung von 
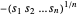(konvex). Formulieren Sie das Problem unter Verwendung der Hilfsvariable 
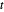mit einer linearen Zielfunktionn -
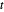mit den zusätzlichen Einschränkungen 
.
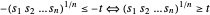Das Problem ist das folgende:
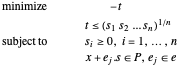
Der konvexe Kegel ist die Menge von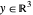 
so dass 
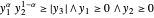und kann in der Wolfram Language durch 
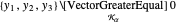ausgedrückt werden.
Da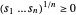 
, kann die neue Einschränkung 
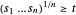für nichtnegative 
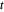erfüllt werden und ist äquivalent mit 
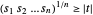. Dies kann als eine Reihe von konvexen Kegeln formuliert werden:
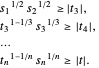
Bei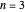 
ist das Problem das folgende:
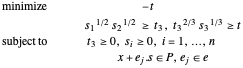
Ein konvexes Polyeder kann als Schnittpunkt von Halbräumen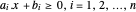 
dargestellt werden. Extrahieren Sie die Koeffizienten 
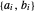für jede Seite.
Lösen Sie das Problem.
Visualisieren Sie den eingeschriebenen Quader mit maximalem Volumen.
Anstelle eines Polyeders nehmen Sie eine konvexe konisch darstellbare Menge K⊆n—zum Beispiel ein Ellipsoid. Eine Ecke des Quaders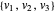 
befindet sich innerhalb des Ellipsoids wenn 
.
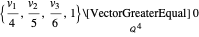Lösen Sie das Problem.
Plotten Sie das Ergebnis.
