Optimierte Fachwerksplanung
Entwerfen Sie ein Fachwerk mit minimaler Last, das an einem Ende an der Wand verankert ist und am anderen Ende einer Belastung standhalten muss.
Dieses Beispiel zeigt, wie viele Funktionen der Wolfram Language zusammen verwendet werden können, um eine symbolische Form eines linearen Optimierungsproblems zu bilden, das durch LinearOptimization effizient gelöst werden kann.
Wählen Sie einige spezifische Positionen, an denen das Fachwerk an der Wand verankert ist.
Die Position, an der die Last aufgebracht wird, befindet sich am Ende des Tragwerks.
Das Tragwerk kann durch Verbindungen und Knotenpunkt modelliert werden. Jeder Knotenpunkt ist über eine Verbindung mit einem benachbarten Knoten verbunden. Ein mögliches Verbindungsmuster ist hier angegeben.
Die Kandidatenknoten werden in einem rechteckigen Gitter platziert.
Visualisieren Sie die Knotenpositionen, die Ankerpunktpositionen, die Position, an der die Last aufgebracht wird, und die Verbindung eines einzelnen Knotenpunkts in der Mitte des Tragwerks.
Jedem Knotenpunkt ist einem eindeutigen Index zugeordnet. Die Association liefert eine schnelle Nachschlagetabelle.
Ermitteln Sie die Indizes, die mit Anker- und Kraftpunkten verknüpft sind.
Konstruieren Sie eine Funktion, die die Verbindung eines beliebigen Gitterpunktes für ein bestimmtes Konnektivitätsmuster liefert.
Verwenden Sie für einen bestimmten Knotenpunkt 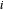 die Konnektivität, um um zu bestimmen, welche Verbindungen diesen Knoten enthalten. Wenn die Knoten
die Konnektivität, um um zu bestimmen, welche Verbindungen diesen Knoten enthalten. Wenn die Knoten 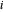 und
und 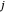 verbunden sind, dann stellen
verbunden sind, dann stellen 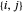 und
und 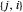 dieselbe Verbindung dar. Um Wiederholungen zu vermeiden, sollten Sie nur die Verbindung mit
dieselbe Verbindung dar. Um Wiederholungen zu vermeiden, sollten Sie nur die Verbindung mit 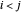 berücksichtigen.
berücksichtigen.
Beschreiben Sie die Menge der Verbindungen durch ℒ, sodass wenn Knoten 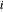 und Knoten
und Knoten 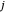 eine Verbindung bilden, dann
eine Verbindung bilden, dann 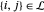 .
.
Angenommen, die Dicke einer Verbindung und damit die Masse pro Längeneinheit muss proportional zur Kraft sein, die auf diese Verbindung ausgeübt wird. Eine bequeme Möglichkeit, die Verbindung ℒ zu beschreiben, besteht darin, eine Indexierung der Links durchzuführen, so dass es für jedes verbundene Paar 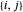 einen eindeutigen Index
einen eindeutigen Index 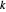 mit
mit 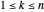 gibt.
gibt.
Das Ziel ist es, 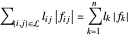 zu minimieren, wobei
zu minimieren, wobei 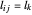 die Länge der Verbindung zwischen den Knoten
die Länge der Verbindung zwischen den Knoten 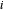 und
und 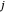 mit Index
mit Index 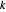 ist und
ist und 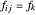 die Kraft ist, die von der Verbindung auf ihre Endgelenke ausgeübt wird.
die Kraft ist, die von der Verbindung auf ihre Endgelenke ausgeübt wird.
Die Funktion 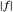 ist nichtlinear, kann aber als lineare Funktion ausgedrückt werden, indem
ist nichtlinear, kann aber als lineare Funktion ausgedrückt werden, indem 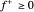 und
und 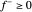 festgelegt werden, dass
festgelegt werden, dass 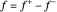 und
und 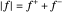 . Die Zielfunktion ist
. Die Zielfunktion ist 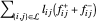 .
.
An keinem Knoten außer dem Kraftpunkt werden externe Kräfte angewendet.
Am Kraftpunkt wird eine vertikale Einheitskraft nach unten aufgebracht.
An jedem nicht verankernden Knoten 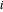 muss ein Kraftausgleich vorhanden sein
muss ein Kraftausgleich vorhanden sein 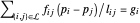 , wobei
, wobei 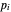 die Position des Knotens
die Position des Knotens 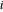 und
und 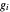 die externe Kraft am Knoten
die externe Kraft am Knoten 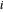 ist. Definieren Sie eine Funktion, die die Kraftausgleichsbeschränkung für Knoten
ist. Definieren Sie eine Funktion, die die Kraftausgleichsbeschränkung für Knoten 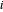 ist.
ist.
Verwenden Sie Complement, um die Ankerknoten nicht einzubeziehen.
Die letzten Einschränkungen sind:
Lösen Sie das resultierende System.
Visualisieren Sie das optimierte Tragwerk. Verwenden Sie Blautöne, die die Spannung der Verbindungen darstellen und Rottöne, die die Ausdehnung anzeigen.