Zuweisungsprobleme
Ermitteln Sie die Strommenge, die ein Unternehmen von seinen vier Kraftwerken in fünf Städte transportieren muss, um den Gewinn zu maximieren und die Kosten zu minimieren und gleichzeitig den Spitzenbedarf der Städte zu decken.
Dieses Beispiel zeigt, wie LinearFractionalOptimization verwendet werden kann, um das Verhältnis von Kosten zu Gewinn innerhalb bestimmter Grenzen zu minimieren. Die Verwendung einer matrixwertigen Variablen macht die Modellierung relativ einfach.
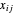sei die Menge an Strom, die von Kraftwerk 
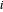an die Stadt 
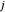geschickt wird. Die Gesamtkosten für den Transport von Strom ist 
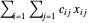, wobei 
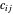die Kosten für den Transport von Strom vom Kraftwerke 
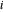zur Stadt 
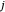ist. Total[m, 2] ergibt die Summe aller Elemente einer Matrix 
.
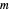Der Gesamtgewinn des Energieversorgers ist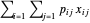 
, wobei 
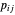der Gewinn vn Kraftwerk 
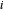durch den Verkauf von Strom an Stadt 
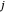ist.
Der gesamte Strom, der von jeder Anlage gesendet wird, sei durch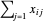 
gegeben und muss größer oder gleich dem Mindeststrom sein, den die Anlage liefern kann. Total[x, {2}] ergibt den Betrag für jede Zeile von 
.
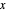Der gesamte Strom, der an jede Stadt geschickt wird, sei durch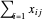 
gegeben und muss größer sein als die Mindestnachfrage und kleiner als oder gleich wie der Höchstbedarf. Total[x, 1] ergibt den Betrag der Spalten von 
.
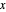Die Kraftwerke können nur Strom liefern und keinen Strom aus den Städten erhalten. VectorGreaterEqual kann verwendet werden, um anzugeben, dass alle Elemente der Matrixvariablen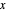 
größer oder gleich Null sein sollen.
Als Beispiel seien hier die Kosten für den Transport von einer Million Kilowattstunden (kWh) Strom von vier Kraftwerken in fünf Städte genannt.
Der Gewinn, den jedes Kraftwerk durch den Verkauf von 1 Mio. kWh an jede Stadt erzielt, ist hier dargestellt.
Der jeweilige Spitzenbedarf der Städte ist 45, 20, 30, 30 und 40 Mio. kWh, während der Mindestbedarf bei 5 Mio. kWh liegt.
Die Kraftwerke können jeweils mindestens 35, 50, 40 und 40 Mio. kWh Strom liefern.
Die optimale Menge an Strom, die jedes Kraftwer in jede Stadt liefern muss, kann gefunden werden, indem das Verhältnis von Kosten zu Gewinn minimiert wird.
Nachstehend die Aufteilung der Stromversorgung in Tabellenform.
