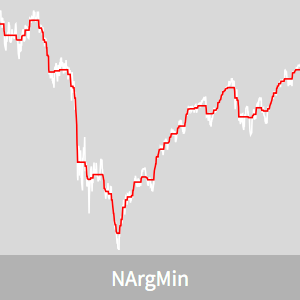
構造保持平滑化
全変動フィット正則化を使うと，フィルタで信号のノイズを除去すると同時に，重要なジャンプを保持することができる．
この例題では、Wolfram言語関数でのモデリングが，NArgMinを使った自然な方法で全変動フィット正則化を実装するのにいかに簡単に使えるかを示す．
信号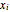 
の場合，この操作は
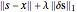を最小化する値 
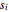を求めることで行うことができる．ここで 
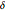s は成分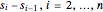 
のベクトル，λ はノイズの軽減と信号 
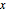への近似の間のトレードオフに使われるパラメータである．
2008年の金融危機の間のダウ平均株価を考えてみる．日によってかなりの乱高下が見られるが，これは長い目で見れば事実上ノイズと考えることができる．
信号は，株価指数の値の列である．
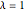の平滑化指標を求める．Method->"Convex"を使う．他の方法では，これほど多数の変数が扱えたとしても非常に遅くなるからである．
平滑化指標と実際の指標を比較する．
平滑化指数は主なトレンドを示すが，重要な特徴を見逃している．特徴を感知することと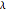 
によって決定される平滑化の程度との間にはトレードオフがある．
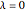のときは，平滑化はなく 
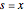である．しかし 
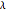が∞に近付くにつれて，
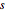は一定信号に近付く．全変動と 
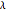のさまざまな値に対するもとの信号からの偏差のプロットで，最高のバランスを達成するための適切な 
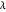の値が示される．
曲線の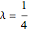
付近で著しく折れ曲がっている．これは妥当なバランスが達成されたことを示す．
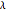の別の値のいくつかに対する平滑化指標を見るのもおもしろい．
正規化を使った最小二乗法を行うことで，最小化を考えることもできる．Fitで新しいオプションFitRegularizationを使うと，これを行うことができる．
