Lissage préservant la structure
La régularisation de l'ajustement de variation totale peut être utilisée pour filtrer le bruit dans un signal tout en préservant les sauts qui sont significatifs.
Cet exemple démontre comment une modélisation simple en termes de fonctions Wolfram Language peut être utilisée pour implémenter la régularisation de l'ajustement de variation totale de manière naturelle en utilisant NArgMin.
Pour un signal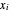 
, il suffit de trouver des valeurs 
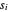qui minimisent 
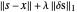, où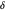 
correspond au vecteur avec les éléments 
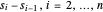, et λ correspond à un paramètre qui est utilisé pour faire un compromis entre la réduction du bruit et la proximité du signal 
.
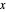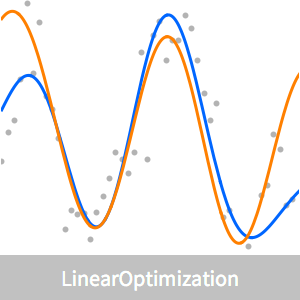
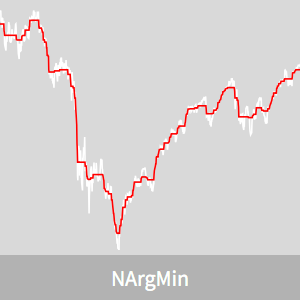
Prenons l'exemple de l'indice boursier Dow Jones Industrial Average pendant la crise financière de 2008. Il y a beaucoup de volatilité quotidienne qui, à long terme, peut être considérée comme du bruit.
Le signal correspond à la séquence des valeurs de l'indice boursier.
Trouvez l'indice lissé pour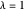 
. Method->"Convex" est utilisé, car d'autres méthodes seraient très lentes si elles avaient la chance d'aboutir avec autant de variables.
Comparez l'indice lissé avec l'indice réel.
L'indice lissé montre les principales tendances mais omet certaines caractéristiques importantes. Il y a un compromis entre les caractéristiques de capture et le lissage qui est déterminé par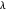 
. Pour 
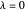, il n'y a pas de lissage et 
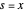. D'autre part, lorsque 
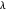se rapproche de ∞, 
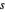se rapprochera d'un signal constant. Un tracé de la variation totale par rapport à l'écart du signal original pour différentes valeurs de 
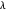peut donner une indication des valeurs appropriées de 
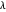pour obtenir le meilleur équilibre.
Il y a une courbure apparente dans la courbe autour de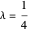 
, ce qui indique que l'on atteint un équilibre raisonnable.
Il est intéressant d'examiner l'indice lissé pour certaines des diverses valeurs de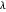 
.
La minimisation peut aussi se concevoir en termes d'ajustement des moindres carrés avec la régularisation. La nouvelle option FitRegularization peut être utilisée dans Fit pour cela.
