可视化平面曲线及其属性
"PlaneCurve" 实体域中提供了许多平面曲线和大量预先计算的属性。
例如,很容易获取参数化曲线的几何属性。
形式变量(绘制为下面有一个点的字母,如 t)用于表示依赖于参数的属性中的函数槽。然后通过简单的替换即可为特定参数赋值,如下所示。
曲线的可视化及其属性也很容易实现。下面用参数化方程绘制三叶曲线,并标出曲线各个点(红点)上的法线(绿色箭头)和切线(蓝色箭头)。
同样,可以基于给定属性(如曲率)对曲线着色。
用蓝色、紫色和红色标示曲率最大的区域。
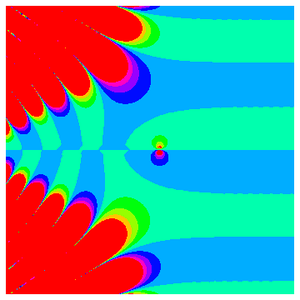
下面来看众所周知的圆的笛卡尔方程,我们可以看到更加多彩的图形。
提取等式取决于坐标位置的部分,然后将半径作为缩放常数,构建圆形的层级曲线。
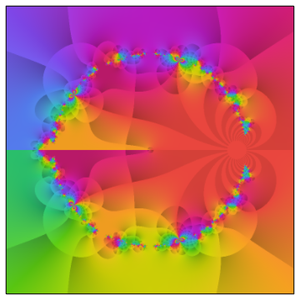
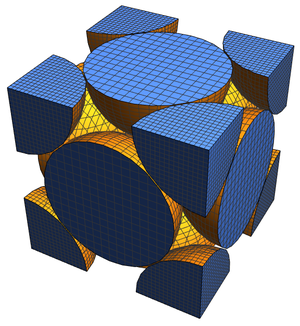
填充正方形的边界也可以用笛卡尔方程来表示。
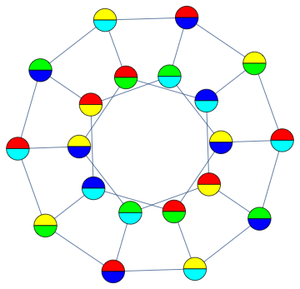
在 "PlaneCurve" 领域,这种表示一直到六边形都是可行的。
构造这种表示的过程可以推广到产生任何多边形层级曲线。