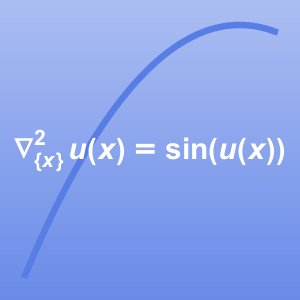Covariant affine de Newton
Utilisez le nouvel algorithme covariant affine de Newton pour trouver les racines des grands systèmes d'équations.
Discrétisez l'équation différentielle non linéaire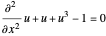 
avec une méthode de différence finie.
Définissez le jacobien du système d'équations discrétisées.
Définissez une valeur initiale pour l'algorithme de recherche des racines.
Inspectez le nombre d'étapes, d'évaluations et d'évaluations jacobiennes nécessaires pour trouver la racine du système d'équations.
Comparez à la nouvelle méthode covariante affine de Newton récemment mise en œuvre :
La méthode covariante affine de Newton réduit considérablement le nombre d'évaluations jacobiennes nécessaires pour trouver la racine. Puisque la construction et l'évaluation du jacobien peut prendre du temps pour de grands systèmes d'équations, la méthode covariante affine de Newton permet d'accélérer le processus de recherche des racines.
Pour plus d'informations sur la méthode covariante affine de Newton, reportez-vous à la documentation.
