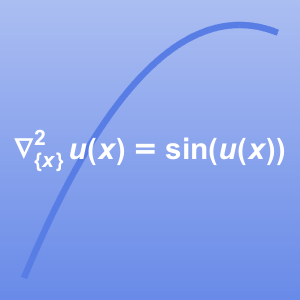Affines kovariantes Newton-Verfahren
Nutzen Sie den neuen affinen kovarianten Newton-Algorithmus, um die Nullstellen großer Gleichungssysteme zu finden.
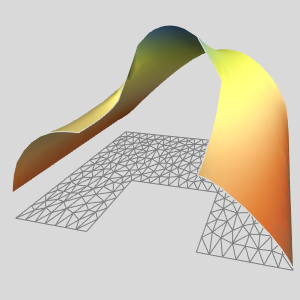
Diskretisieren Sie die nichtlineare Differentialgleichung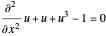 
mit einer finiten Differenzenmethode.
Definieren Sie die Jacobi-Determinante des diskretisierten Gleichungssystems.
Legen Sie einen Anfangswert für den Algorithmus zum Finden der Nullstelle fest.
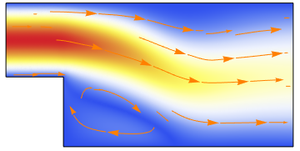
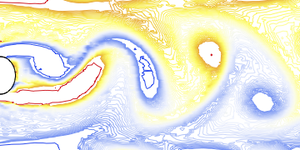
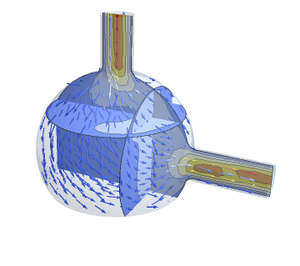
Untersuchen Sie die Anzahl der Schritte, Auswertungen und Jacobi-Auswertungen, die erforderlich sind, um die Nullstelle des Gleichungssystems zu finden.
Vergleichen Sie dies mit der neu implementierten affinen kovarianten Newton-Methode.
Die affine kovariante Newton-Methode reduziert die Anzahl der Jacobian-Evaluierungen, die benötigt werden, um die Nullstelle zu finden, um ein Wesentliches. Da das Erstellen und die Evalueirung der Jacobi-Determinante für große Gleichungssysteme zeitaufwendig sein kann, hilft die affine kovariante Newton-Methode, den Nullstellensuchprozess zu beschleunigen.
Weitere Details zur affinen kovarianten Newton-Methode finden Sie in der Dokumentation.
