Transporte de energia
Resolva um problema de multi-física que associa a equação de Navier-Stokes a uma equação de calor:
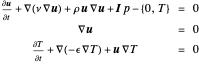
Aqui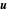 
é o campo de velocidade com valor vetorial, 
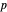é a pressão e 
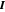a matriz de identidade. 
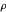e 
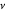são a densidade e a viscosidade dinâmica, respectivamente. 
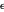é a capacidade térmica do líquido e 
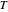a temperatura.
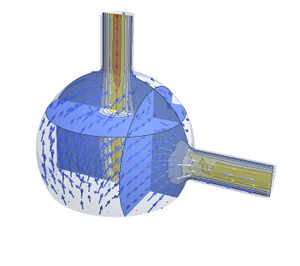
Especifique parâmetros e uma região retangular com recortes.
Visualize a região.
Especifique um número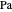 
e um número Rayleigh 
.
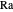Defina uma equação de viscosidade de Navier-Stokes que seja acoplada a uma equação de calor usando uma aproximação de Boussinesq. Use os parâmetros do material especificados.
Configure condições de contorno anti-deslizantes para as velocidades em todas as paredes de contorno.
Defina um ponto de pressão de referência.
Especifique uma diferença de temperatura entre as paredes esquerda e direita.
Substitua os parâmetros nas condições de contorno.
Defina as condições iniciais para que o sistema esteja em repouso.
Monitore o progresso de integração no tempo e o tempo total necessário para resolver a equação diferencial parcial , usando um espaçamento de malha especificado e interpolando as velocidades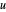 
e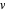 
, a temperatura 
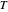na segunda ordem e a pressão 
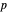na primeira ordem.
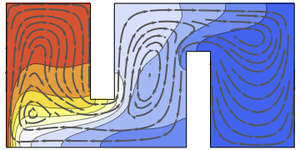
Construa uma visualização dos contornos da região.
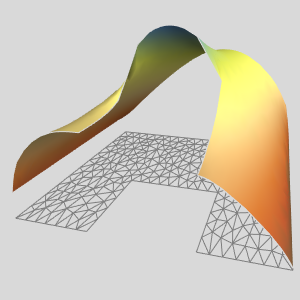
Visualize a distribuição da pressão.
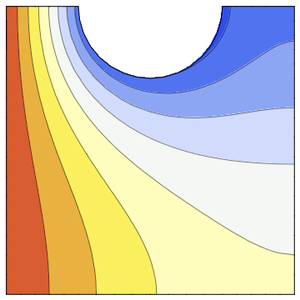
Visualize a distribuição da temperatura.
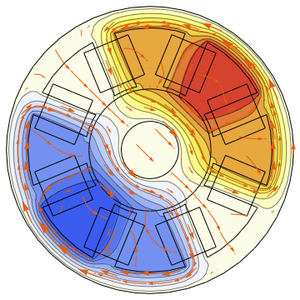
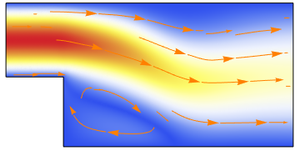
Visualize o campo de velocidade.
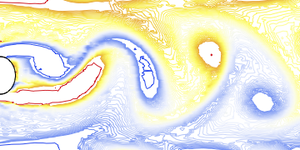
Anime a mudança de temperatura e as linhas de fluxo de velocidade.
Para os curiosos, examine os diferentes campos de velocidade produzidos simplesmente trocando as posições de recorte.
