Modélisez les lignes de champ d'une plaque triangulaire chargée
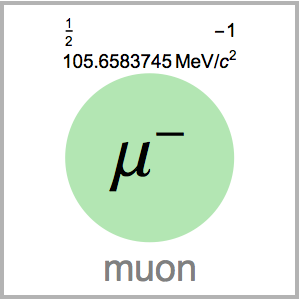
Wolfram Language est à la fois un langage informatique puissant et efficace pour faciliter la communication scientifique chez les gens. Le domaine d'entités des systèmes physiques en est un bon exemple. Pour avoir une idée de l'étendue des possibilités disponibles avec "PhysicalSystem", examinez un échantillon d'entités disponibles :
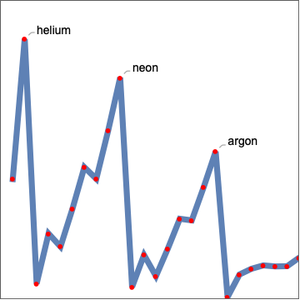
La catégorisation en classes d'entités simplifie la recherche d'un système physique particulier. Il existe actuellement 27 classes d'entités non disjointes, dont vous trouverez un exemple ci-dessous.
Plutôt que de contenir principalement des données numériques ou textuelles, comme dans le domaine "Country" par exemple, le domaine du système physique contient principalement des formules comme celles qu'on pourrait trouver dans un manuel scolaire. Pour voir comment l'utiliser, prenons par exemple le système de plaques triangulaires chargées.
Vous pouvez facilement voir ce qui est disponible pour cette entité en appelant "NonMissingProperties".
En général, les entités du domaine "PhysicalSystem" sont associées à un ensemble de "variables du système" qui décrivent les paramètres physiques globaux du système. Pour la plaque triangulaire dans l'espace, voici la charge, 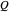 , de la plaque et les coordonnées de ses sommets
, de la plaque et les coordonnées de ses sommets  pour
pour 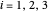 .
.
Toute propriété donnée peut dépendre des variables de ce système et éventuellement des coordonnées généralisées du système. Par exemple, en regardant la densité de charge électrique, vous avez ce qui suit.
Remarque ! Comme c'est souvent le cas pour les formules renvoyées par "PhysicalSystem", la tête de cette expression est Inactive[ReplaceRepeated]. Cela permet d'utiliser des variables intermédiaires, pouvant rendre ces expressions plus petites et plus faciles à comprendre. Par exemple, dans la formule présentée précédemment, 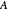 correspond à l'aire du triangle et
correspond à l'aire du triangle et 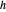 représente la distance perpendiculaire du triangle au point de mesure. Les éléments DiracDelta et Piecewise représentent le fait que la densité de charge n'est pas nulle uniquement sur la plaque triangulaire (infiniment mince). Lors de l'activation du remplacement, l'expression se réduira à une expression impliquant uniquement les variables du système et les coordonnées généralisées.
représente la distance perpendiculaire du triangle au point de mesure. Les éléments DiracDelta et Piecewise représentent le fait que la densité de charge n'est pas nulle uniquement sur la plaque triangulaire (infiniment mince). Lors de l'activation du remplacement, l'expression se réduira à une expression impliquant uniquement les variables du système et les coordonnées généralisées.
Une propriété plus intéressante à examiner pourrait être le champ électrique de la plaque chargée. Pour une visualisation simplifiée, considérez des plaques en deux dimensions (en prenant 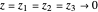 ). La forme du champ peut être trouvée en appelant l'EntityValue suivante (le résultat est supprimé ici car il est assez grand).
). La forme du champ peut être trouvée en appelant l'EntityValue suivante (le résultat est supprimé ici car il est assez grand).
En choisissant un triangle intéressant, en substituant ses coordonnées de sommets en fieldForm et en l'activant, on obtient une solution simple, quoique complexe, de forme fermée pour le vecteur de champ électrique, en fonction des coordonnées dans le plan 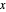 -
-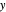 .
.
L'expression précédente est assez compliquée, donc pour faciliter l'affichage, vous pouvez la restituer dans un TraditionalForm Pane.
En guise de dernière étape, essayez de visualiser les lignes de champ qui découlent de ces formules. Heureusement, Wolfram Language dispose de la fonction intégrée StreamDensityPlot pour y parvenir. Vous devez faire un peu attention en vous débarrassant des éléments QuantityVariable de l'expression précédente avant de pouvoir la représenter dans un graphique. Les remplacements que vous pouvez utiliser pour le faire sont démontrés ci-dessous. De plus, pour faire une représentation graphique plus intéressante, superposez deux triangles chargés et créez un Manipulate montrant comment leurs champs interagissent à mesure que leur position, leur angle et leurs charges relatives sont modifiés. Visualisez le code et l'animation obtenue, et prenez plaisir à faire des expériences pour simuler des systèmes physiques dans Wolfram Language !