Élargissement des estimations de distributions matricielles
La version 11 a introduit des matrices aléatoires, étroitement intégrées dans le cadre de probabilités et de statistiques. Les matrices aléatoires sont utilisées dans une étonnante variété de domaines dont les statistiques, la physique, les mathématiques pures, la biologie et la finance, entre autres. La version 12 complète la prise en charge des matrices aléatoires avec estimation pour MatrixNormalDistribution, MatrixTDistribution, WishartMatrixDistribution et InverseWishartMatrixDistribution.
WishartMatrixDistribution[ν, Σ] représente la distribution de la covariance de l'échantillon à partir de  réalisations indépendantes d'une distribution gaussienne multivariée avec une matrice de covariance
réalisations indépendantes d'une distribution gaussienne multivariée avec une matrice de covariance 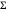 , lorsque le degré du paramètre de liberté
, lorsque le degré du paramètre de liberté 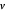 est un nombre entier.
est un nombre entier.
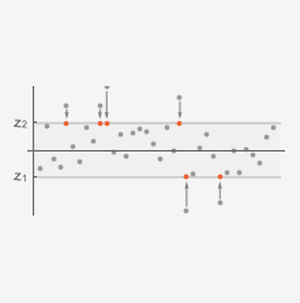
Simulez m échantillons aléatoires de longueur n à partir de MultinormalDistribution.
Calculez la covariance de l'échantillon pour chaque liste.
Le résultat est une liste de n matrices.
Ajustez WishartMatrixDistribution à l'échantillon de covariance.
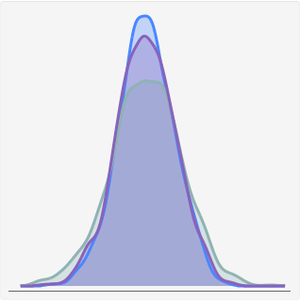
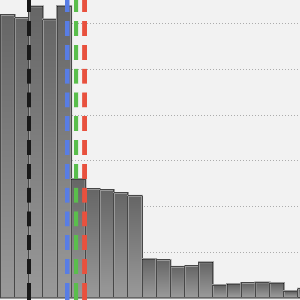
Comparez la moyenne de la distribution ajustée avec la moyenne des covariances de l'échantillon.
Comparez les variances.
Pour une matrice 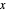 , distribuée en tant que WishartMatrixDistribution[ν, Σ], l'inverse
, distribuée en tant que WishartMatrixDistribution[ν, Σ], l'inverse 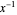 est distribué en tant que InverseWishartMatrixDistribution[ν, Σ-1].
est distribué en tant que InverseWishartMatrixDistribution[ν, Σ-1].
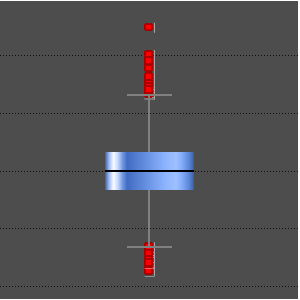
Calculez l'inverse des covariances de l'échantillon et ajustez InverseWishartMatrixDistribution.
Vérifiez si la matrice de covariance de la distribution matricielle estimée de Wishart correspond à l'inverse du modèle inverse de Wishart.