Estimativa estendida de distribuições de matrizes

A versão 11 introduziu matrizes aleatórias, que foram estreitamente integradas à estrutura de probabilidade e estatística existente. Matrizes aleatórias têm usos em uma surpreendente variedade de campos, incluindo estatística, física, matemática pura, biologia e finanças, entre outros. A versão 12 completa o suporte para matrizes aleatórias com estimativa para MatrixNormalDistribution, MatrixTDistribution, WishartMatrixDistribution e InverseWishartMatrixDistribution.

WishartMatrixDistribution[ν, Σ] é a distribuição da covariância da amostra das realizações independentes 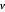de uma distribuição multivariada gaussiana com matriz de covariância 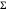quando o parâmetro de graus de liberdade 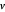é um número inteiro.

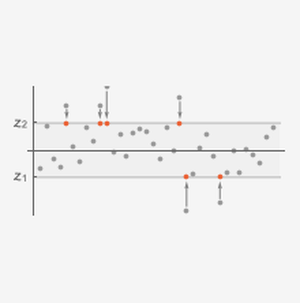
Simule m amostras aleatórias de comprimento n de uma MultinormalDistribution.

Calcule a covariância da amostra para cada lista.

O resultado é uma lista de n matrizes.

Ajuste WishartMatrixDistribution para a amostra de covariância.

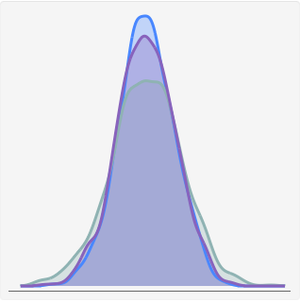
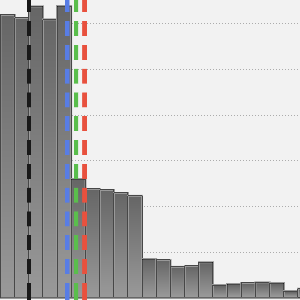
Compare a média da distribuição ajustada com a média das covariâncias da amostra.

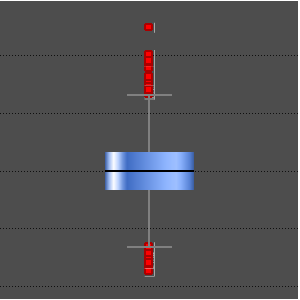
Compare as variações.

Para uma matriz 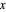distribuída como WishartMatrixDistribution[ν, Σ], o inverso 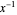é distribuído como InverseWishartMatrixDistribution[ν, Σ^-1].

Calcule o inverso das covariâncias da amostra e ajuste um InverseWishartMatrixDistribution.

Verifique se a matriz de covariância da distribuição da matriz Wishart estimada é o inverso do modelo Wishart inverso.