Élargissement des tests d'hypothèse pour l'équivalence de dispersion
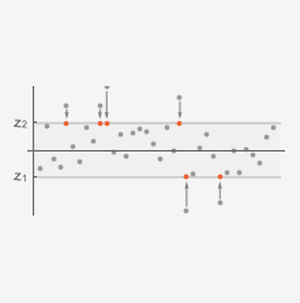
Les fonctions BrownForsytheTest, ConoverTest et LeveneTest ont été élargies pour permettre de tester l'hypothèse d'équivalence de dispersion avec plusieurs échantillons.
Les tests de Brown-Forsythe et de Levene supposent que les données sont distribuées normalement, tandis que le test de Conover présente des conditions plus souples et émet pour seule hypothèse que les jeux de données sont symétriques par rapport à une moyenne commune.
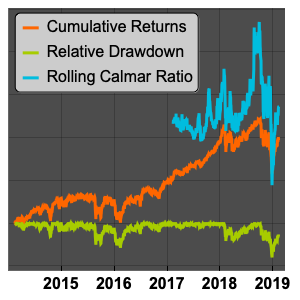
Comparez la variance des changements quotidiens de l'indice S&P 500 sur quelques années.
Créez des séries temporelles annuelles.
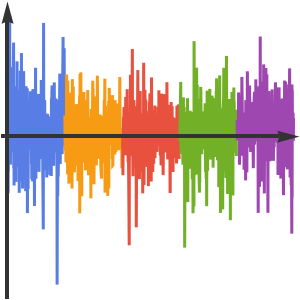
Calculez les différences journalières pour chaque série temporelle annuelle.
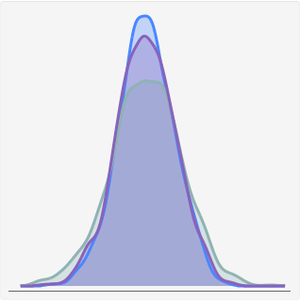
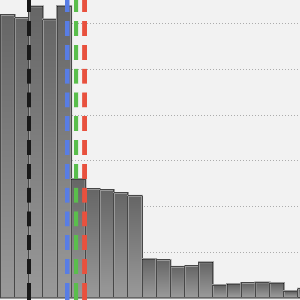
Évaluez si les séries temporelles représentant ces différences sont distribuées normalement.
Étant donné que tous les échantillons ne sont pas distribués normalement, de nombreux tests de variance ne sont pas nécessaires. Vérifiez les hypothèses du test de Conover.
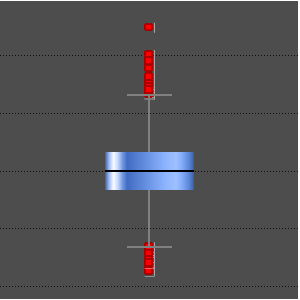
Vous pouvez supposer que chaque série temporelle est symétrique autour de 0 : les graphiques précédents montrent une symétrie autour de 0 et les médianes sont suffisamment proches de 0.
Utilisez le test de Conover pour évaluer si toutes les séries temporelles ont la même variance.
Vous pouvez en conclure que la variance des changements de cours journaliers n'est pas la même pour chacune des périodes observées.