相関測定
測定値の分析において，不確かさが相関する値の集合が生成されることがよくある．これらの値を使って計算をするときは，この相関を考慮しなければならない．
この例では，Guide to the Expression of Uncertainty in Measurement（測定における不確かさの表現のガイド）ドキュメントのH.3に従っている．この例は，最小二乗フィットを使った温度計の線形キャリブレーションの過程を説明している．
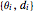ペアの集合を取る．
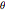は
との摂氏の温度差，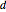
は正しい結果からの偏差である．
最良の線形フィットを計算する．
次は．フィットのパラメータとその推定される不確かさである．
次は，フィットの共分散行列と相関行列である．値の間に，相関行列の非零の非対角要素で表された，非零の相関があるのが分かる．
これらは次のような関係にある．
不確かさの推定を使って摂氏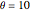 
度との温度差を推定するのなら，独立したAroundオブジェクトに基づいた以下のどちらの計算も正しくないだろう．
これら2つの同等の計算は，フィットのパラメータ間の不確かさの相関を無視している．相関を考慮すると，パラメータはVectorAround式を使って表される．
