ゲージのキャリブレーション

測定における不確かさを扱う際の基本的なステップの一つは，導き出された大きさの不確かさを得るための数式によるその不確かさの伝播である．

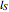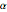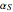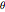この例はGuide to the Expression of Uncertainty in Measurement（測定における不確かさの表現のガイド）ドキュメントのH.1に従っている．この例は，で長さ の標準ゲージと比較することで，エンドゲージの長さ のキャリブレーションを説明している．両者はそれぞれ と の熱膨張係数を有し，測定は，どちらも基準温度との違いである温度 と 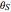で行われる．

すると，長さの違いは次のようになる．

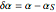と 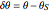を定義すると，次のように を近似することができる．この方程式の右辺の変数はすべて，もはや相関していない．

標準エンドゲージのキャリブレーション証明書には，におけるこの値が示されている．

熱膨張係数は以下のように推定される．

そして，次が温度差である．

最後に，次が長さの差 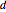について与えられる値である．

したがって，エンドゲージは温度でこの長さになる．

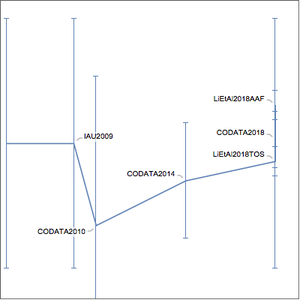
50.000838㎜という長さが32nmの不確かさとともに得られたが，これは前掲文書の値を正確に再現している．