Matrices antisimétricas y ortogonales
Si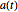 
es una matriz antisimétrica y 
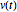es un vector que obedece la ecuación diferencial 
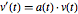, entonces 
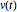tiene una magnitud constante. Considere primero una matriz constante.
| In[1]:= |  X |
| In[2]:= |  X |
| Out[2]= |  |
La solución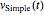 
a la ecuación diferencial puede ser escrita usando MatrixExp.
| In[3]:= |  X |
| In[4]:= |  X |
Verifique que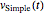 
es de hecho una solución.
| In[5]:= |  X |
| Out[5]= |  |
La matriz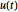 
usada para definir la solución es ortogonal.
| In[6]:= |  X |
| Out[6]= |  |
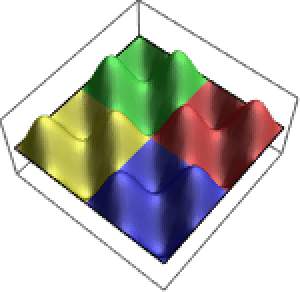
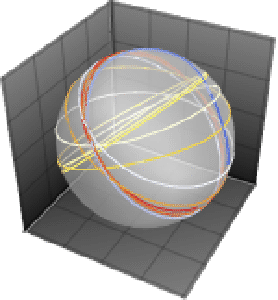
Las soluciones a ecuaciones de coeficientes constantes rastrean círculos que se repiten en la esfera.
| In[7]:= |  X |
| Out[7]= |  |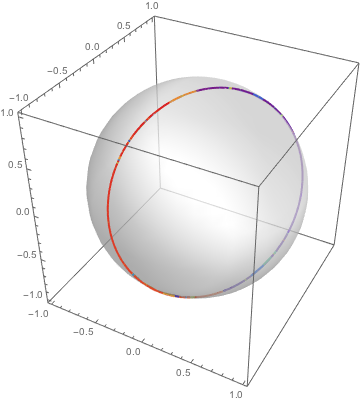
Las soluciones para una matriz de coeficiente no constantes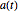 
puede que requieran soluciones numéricas.
| In[8]:= |  X |
| In[9]:= |  X |
| Out[9]= |  |
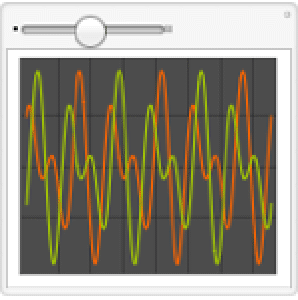
Mientras que el movimiento todavía está restringido a una esfera, patrones más interesantes son ahora posibles.
| In[10]:= |  X |
| In[11]:= |  X |
| Out[11]= |  |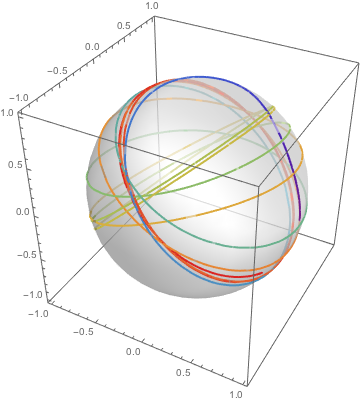
