Matrizes antissimétricas e ortogonais
Se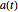 
é uma matriz antissimétrica e 
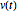é um vetor obedecendo a equação diferencial 
, então 
tem magnitude constante. Considere primeiro uma matriz constante.
| In[1]:= |  X |
| In[2]:= |  X |
| Out[2]= |  |
A solução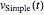 
para a equação diferencial pode ser escrita usando MatrixExp.
| In[3]:= |  X |
| In[4]:= |  X |
Verifique que 
é de fato uma solução.
| In[5]:= |  X |
| Out[5]= |  |
A matriz 
utilizada para definir a solução é ortogonal.
| In[6]:= |  X |
| Out[6]= |  |
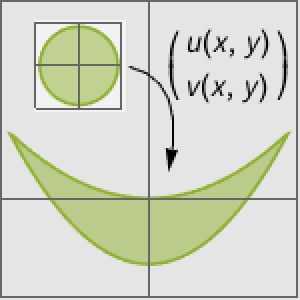
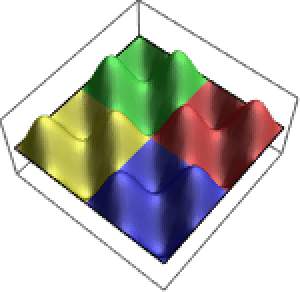
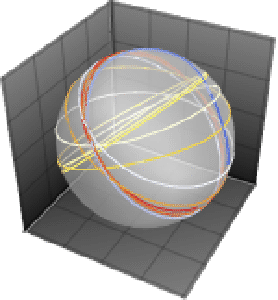
As soluções para equações de coeficientes constantes traçam círculos que se repetem em uma esfera.
| In[7]:= |  X |
| Out[7]= |  |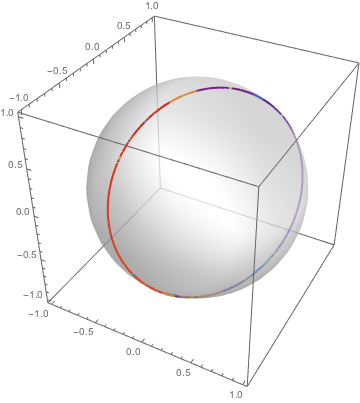
Soluções para uma matriz de coeficientes não constantes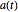 
podem exigir soluções numéricas.
| In[8]:= |  X |
| In[9]:= |  X |
| Out[9]= |  |
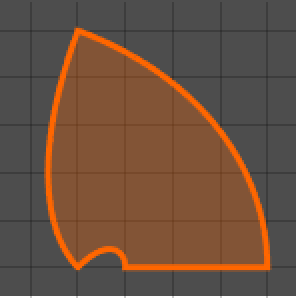
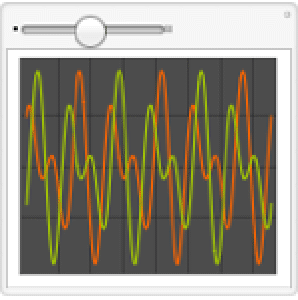
Apesar do movimento ainda estar restrito a uma esfera, padrões mais interessantes são agora possíveis.
| In[10]:= |  X |
| In[11]:= |  X |
| Out[11]= |  |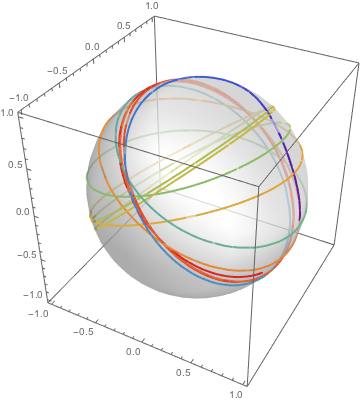
