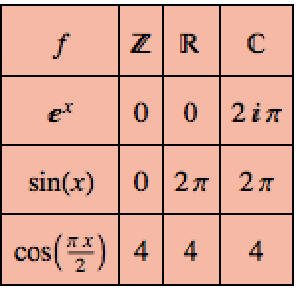反对称和正交矩阵 

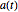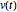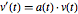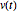如果 是一个反对称矩阵并且 是遵从微分方程 的向量，则 有常量. 首先考虑一个常数矩阵.

In[1]:=

X aSimple[t_] = {{0, 1, 2}, {-1, 0, 3}, {-2, -3, 0}};

In[2]:=

X AntisymmetricMatrixQ[aSimple[t]]

Out[2]=

可以用 MatrixExp 写出微分方程的解 .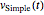

In[3]:=

X u[t_] = MatrixExp[aSimple[t] t];

In[4]:=

X vSimple[t_] := u[t] . {vx, vy, vz};

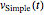验证 确实为解.

In[5]:=

X vSimple'[t] == aSimple[t].vSimple[t] // Simplify

Out[5]=

矩阵 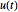用于定义解为正交.

In[6]:=

X OrthogonalMatrixQ[u[t]]

Out[6]=

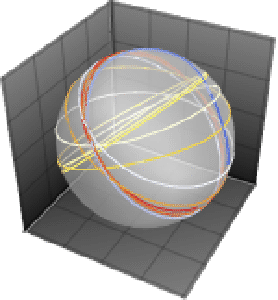
常系数方程组的解在球面上画重复的圆.

In[7]:=

X Block[{vx = 0, vy = 0, vz = 1}, Show[ParametricPlot3D[vSimple[t], {t, 0, 10}, Lighting -> "Neutral", ColorFunction -> (ColorData["Rainbow"][#4] &)], Graphics3D[{Opacity[.5], Sphere[]}], PlotRange -> All, ImageSize -> Medium]]

Out[7]=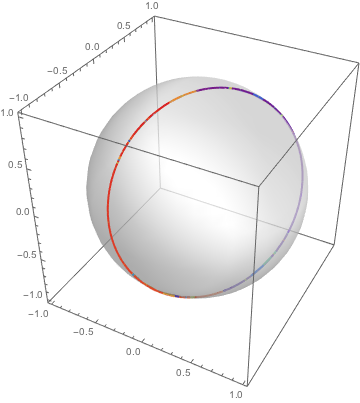

非常系数矩阵 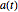的解可能需要数值解.

In[8]:=

X aComplex[t_] := {{0, -t + Sin[t], -Cos[t/2]}, {t - Sin[t], 0, t Cos[t]}, {Cos[t/2], -t Cos[t], 0}}

In[9]:=

X AntisymmetricMatrixQ[aComplex[t]]

Out[9]=

当运动仍限制在球面上，可以得到更多有趣的模式.

In[10]:=

X vComplex = NDSolveValue[{v'[t] == aComplex[t].v[t], v[0] == {1, 0, 0}}, v, {t, 0, 10}];

In[11]:=

X Show[ParametricPlot3D[vComplex[t], {t, 0, 10}, Lighting -> "Neutral", ColorFunction -> (ColorData["Rainbow"][#4] &)], Graphics3D[{Opacity[.5], Sphere[]}], PlotRange -> All, ImageSize -> Medium]

Out[11]=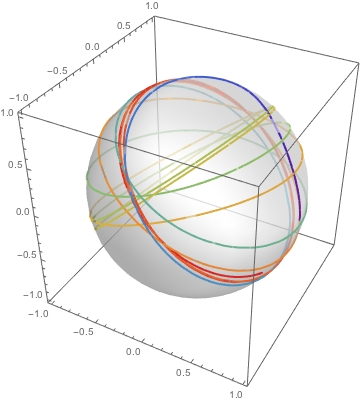