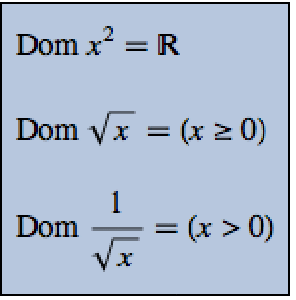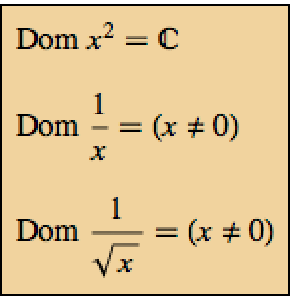反対称行列と直交行列 

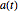が反対称行列で 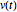が微分方程式 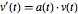,に従うベクトルならば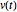，は一定の大きさを持つ．まず定数行列を考える．

In[1]:=

X aSimple[t_] = {{0, 1, 2}, {-1, 0, 3}, {-2, -3, 0}};

In[2]:=

X AntisymmetricMatrixQ[aSimple[t]]

Out[2]=

微分方程式の解 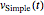はMatrixExpを使って書くことができる．

In[3]:=

X u[t_] = MatrixExp[aSimple[t] t];

In[4]:=

X vSimple[t_] := u[t] . {vx, vy, vz};

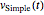が本当に解であることを検証する．

In[5]:=

X vSimple'[t] == aSimple[t].vSimple[t] // Simplify

Out[5]=

解を定義するために使われる行列 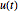は直交行列である．

In[6]:=

X OrthogonalMatrixQ[u[t]]

Out[6]=

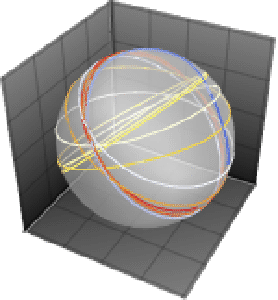
定数係数の方程式の解は，球上に繰り返し円を描く．

In[7]:=

X Block[{vx = 0, vy = 0, vz = 1}, Show[ParametricPlot3D[vSimple[t], {t, 0, 10}, Lighting -> "Neutral", ColorFunction -> (ColorData["Rainbow"][#4] &)], Graphics3D[{Opacity[.5], Sphere[]}], PlotRange -> All, ImageSize -> Medium]]

Out[7]=

非定数係数の行列 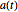の解は数値解を要求する可能性がある．

In[8]:=

X aComplex[t_] := {{0, -t + Sin[t], -Cos[t/2]}, {t - Sin[t], 0, t Cos[t]}, {Cos[t/2], -t Cos[t], 0}}

In[9]:=

X AntisymmetricMatrixQ[aComplex[t]]

Out[9]=

運動はまだ球上に限られるが，もっと面白いパターンが可能になる．

In[10]:=

X vComplex = NDSolveValue[{v'[t] == aComplex[t].v[t], v[0] == {1, 0, 0}}, v, {t, 0, 10}];

In[11]:=

X Show[ParametricPlot3D[vComplex[t], {t, 0, 10}, Lighting -> "Neutral", ColorFunction -> (ColorData["Rainbow"][#4] &)], Graphics3D[{Opacity[.5], Sphere[]}], PlotRange -> All, ImageSize -> Medium]

Out[11]=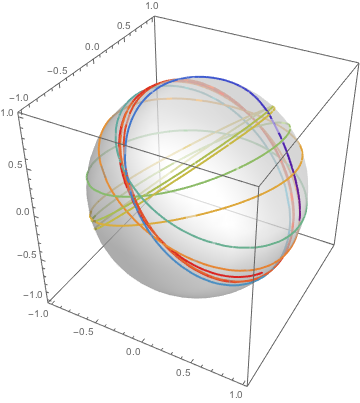