Schiefsymmetrische und orthogonale Matritzen
Wenn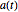 
eine schiefsymmetrische Matrix ist und 
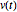ein Vektor, der der Differentalgleichung 
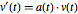gehorcht, dann hat 
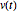eine konstante Länge. Ziehen Sie zuerst eine konstante Matrix in Betracht.
| In[1]:= |  X |
| In[2]:= |  X |
| Out[2]= |  |
Die Lösung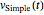 
der Differentialgleichung kann mit MatrixExp aufgeschrieben werden.
| In[3]:= |  X |
| In[4]:= |  X |
Überprüfen Sie, dass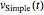 
tatsächlich eine Lösung ist.
| In[5]:= |  X |
| Out[5]= |  |
Die Matrix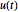 
, die zur Bestimmung der Lösung verwendet wird, ist orthogonal.
| In[6]:= |  X |
| Out[6]= |  |
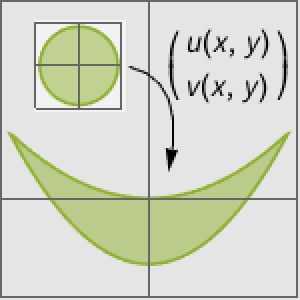
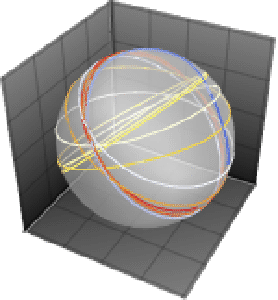
Lösungen für konstante Koeffizientengleichungen erscheinen als Kreise auf der Kugel.
| In[7]:= |  X |
| Out[7]= |  |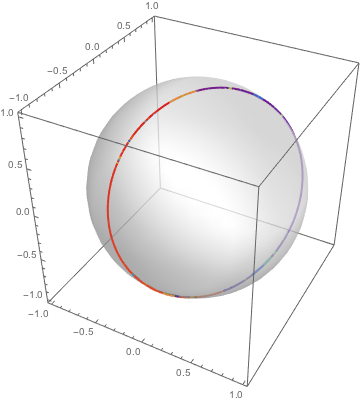
Lösungen für eine nichtkonstante Koeffizientenmatrix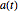 
müssen unter Umständen numerischer Art sein.
| In[8]:= |  X |
| In[9]:= |  X |
| Out[9]= |  |
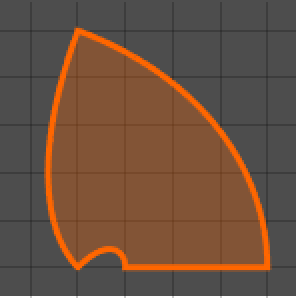
Da sich lediglich die Kugel bewegt, sind nun interessantere Muster möglich.
| In[10]:= |  X |
| In[11]:= |  X |
| Out[11]= |  |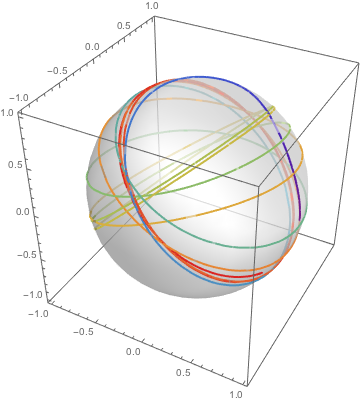
