Die stochastische Exponentialfunktion untersuchen 

Definieren Sie das stochastische Exponential des Wiener-Prozesses als einen transformierten Wiener-Prozess.

In[1]:=

X \[ScriptCapitalE]w = TransformedProcess[E^(w[t] - (\[Sigma]^2 t)/2), w \[Distributed] WienerProcess[0, \[Sigma]], t];

Simulieren Sie den Prozess.

In[2]:=

X data = RandomFunction[\[ScriptCapitalE]w /. \[Sigma] -> 1, {0, 10, 0.01}, 4];

In[3]:=

X ListLinePlot[data, PlotRange -> All]

Out[3]=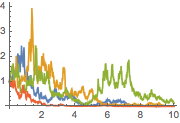

Berechnen Sie den Mittelwert und die Varianz für einen Zeitabschnitt des Prozesses.

In[4]:=

X {Mean[\[ScriptCapitalE]w[t]], Variance[\[ScriptCapitalE]w[t]]}

Out[4]=

Vergleichen Sie dies mit dem Ergebnis unter der Anwendung der entsprechenden stochastischen Differentialgleichung .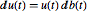

In[5]:=

X \[ScriptCapitalE]sde = ItoProcess[\[DifferentialD]u[t] == u[t] \[DifferentialD]b[t], u[t], {u, 1}, t, b \[Distributed] WienerProcess[0, \[Sigma]]];

In[6]:=

X {Mean[\[ScriptCapitalE]sde[t]], Variance[\[ScriptCapitalE]sde[t]]}

Out[6]=

Definieren Sie das stochastische Exponential des kompensierten Poisson-Prozesses als einen transformierten Poisson-Prozess.

In[7]:=

X \[ScriptCapitalE]p = TransformedProcess[2^p[t] Exp[-\[Lambda] t], p \[Distributed] PoissonProcess[\[Lambda]], t];

In[8]:=

X ListLinePlot[ RandomFunction[\[ScriptCapitalE]p /. \[Lambda] -> 1, {0, 10, 0.01}, 4], PlotRange -> All]

Out[8]=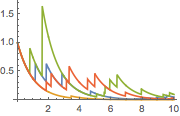

In[9]:=

X {Mean[\[ScriptCapitalE]p[t]], Variance[\[ScriptCapitalE]p[t]]}

Out[9]=