Find Hidden States Underlying Given Emissions of HMM Process
Given the sequence of observations from a system with a known model, it is generically impossible to uniquely recover the corresponding sequence of unobservable states of the system. Mathematica 10 supports two commonly used criteria to find the "optimal" state sequence associated with the given observations—Viterbi decoding and posterior decoding. The Viterbi decoded sequence maximizes the joint likelihood of the sequence of hidden states and emissions. The posterior decoded sequence individually maximizes the likelihood of being in the hidden state for each emission.
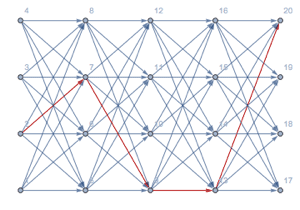
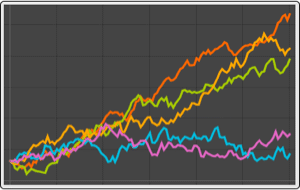
Construct an HMM with left-to-right topology and overlapping emission distributions.
| Out[2]= | 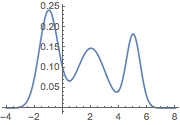 |
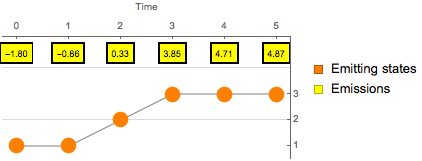
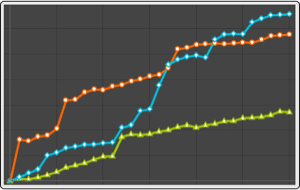
Find the most likely hidden-state sequence using Viterbi decoding.
| Out[4]= | 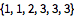 |
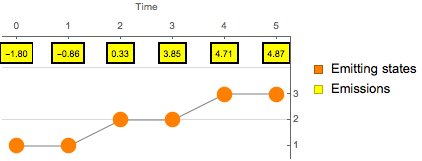
Find the sequence of individually most likely hidden states using posterior decoding.
| Out[5]= | 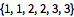 |
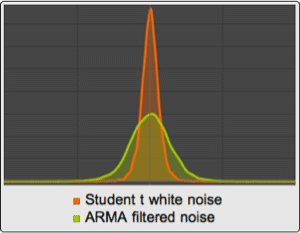
Decoding also works with multivariate emissions.
| Out[7]= | 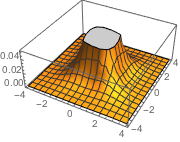 |
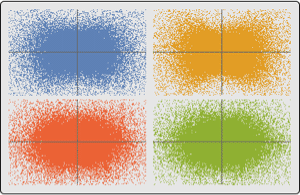
Find the most likely state sequence using Viterbi decoding.
| Out[9]= | 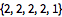 |
Find the sequence of individually most likely states using posterior decoding.
| Out[10]= | 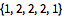 |