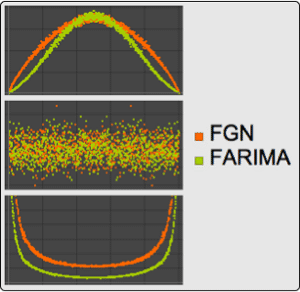
Test for Serial Correlation
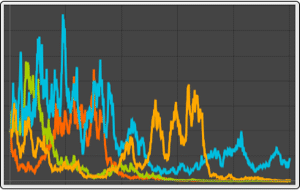
Generate random sample of an ARProcess.
| In[1]:= | X |
The estimated correlation function slowly decreases as a function of lag.
| In[2]:= | X |
| Out[2]= | 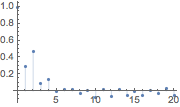 |
Test for serial correlation up to lag 10.
| In[3]:= | X |
| Out[3]= |  |
The tests confirm that data is serially correlated.
| In[4]:= | X |
| Out[4]= |  |
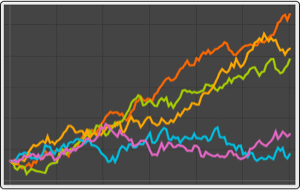
Now generate a random sample from a GARCHProcess.
| In[5]:= |  X |
The values of the estimated correlation function at nonzero lags are very small.
| In[6]:= | X |
| Out[6]= | 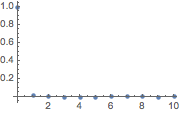 |
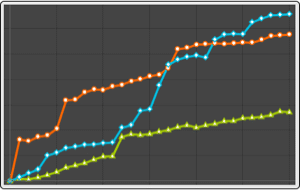
Check the first path with the AutocorrelationTest.
| In[7]:= | X |
| Out[7]= |
| In[8]:= | X |
| Out[8]= |  |
There is no serial correlation, but the slices are not independent.
| In[9]:= | X |
| In[10]:= | X |
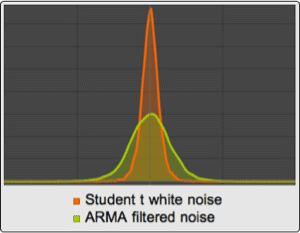
Check the independence between the slice at time zero and the four following slices using Hoeffding's independence test.
| In[11]:= | 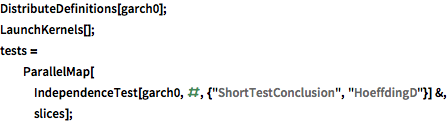 X |
Show scattered plots of slice values at time zero and at other times and the conclusions of the test.
| Out[12]= |  |