Improved Support of Random Processes in Expectation
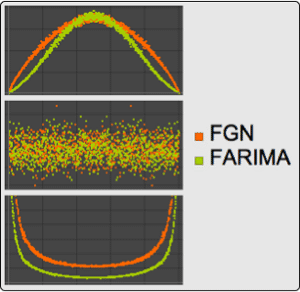
Mathematica 10's improved integration of random process and probability and statistics frameworks enables symbolic computation with many slices of a process. In particular, this example investigates two estimators of the absolute autocorrelation function and explores the trade between the estimator's bias and its population variance.
Let 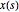 denote values of a random process arma at time
denote values of a random process arma at time  .
.
| In[1]:= | X |
Consider two-sample estimator of the absolute correlation function sequence— 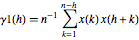 and
and 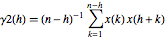 .
.
| In[2]:= | X |
| In[3]:= | X |
Compute population expectation of these estimators for ARMA(1,1) process.
| In[4]:= | X |
| In[5]:= | X |
The first estimator,  , is biased, while the second,
, is biased, while the second, 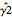 , is unbiased.
, is unbiased.
| In[6]:= | X |
| Out[6]= |
| In[7]:= | X |
| Out[7]= |
Compute population variances of these estimators.
| In[8]:= | X |
| Out[8]= |
| In[9]:= | X |
| Out[9]= |
The variance of the unbiased estimator grows for large lags.
| In[10]:= | X |
| Out[10]= |  |
Therefore, AbsoluteCorrelationFunction uses the biased estimator.
| In[11]:= | X |
| Out[11]= |