Model Option Prices Using Merton Jump-Diffusion  

Define Merton's jump-diffusion model for option pricing.

In[1]:=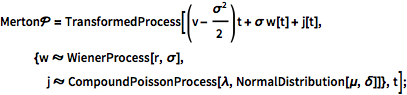

X Merton\[ScriptCapitalP] = TransformedProcess[(v - \[Sigma]^2/2) t + \[Sigma] w[t] + j[t], {w \[Distributed] WienerProcess[r, \[Sigma]], j \[Distributed] CompoundPoissonProcess[\[Lambda], NormalDistribution[\[Mu], \[Delta]]]}, t];

Simulate the process.

In[2]:=

X data = RandomFunction[ Merton\[ScriptCapitalP] /. {v -> 1.2, \[Sigma] -> 0.7, \[Lambda] -> 1.3, \[Mu] -> 0.92, \[Delta] -> 0.425, r -> 1}, {0, 3, 0.02}, 3];

In[3]:=

X ListLinePlot[data]

Out[3]=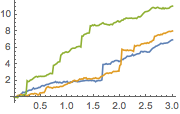

Compute slice properties for the process.

In[4]:=

X {Mean[Merton\[ScriptCapitalP][t]], Variance[Merton\[ScriptCapitalP][t]]}

Out[4]=

Approximate slice distribution from sample.

In[5]:=

X sliceSample = RandomVariate[ Merton\[ScriptCapitalP][ 1] /. {v -> 1.2, \[Sigma] -> 0.7, \[Lambda] -> 1.3, \[Mu] -> 0.92, \[Delta] -> 0.425, r -> 1}, 10^6];

In[6]:=

X SmoothHistogram[sliceSample]

Out[6]=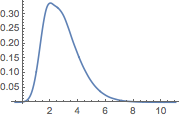