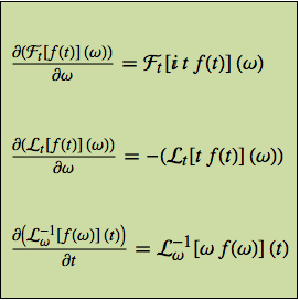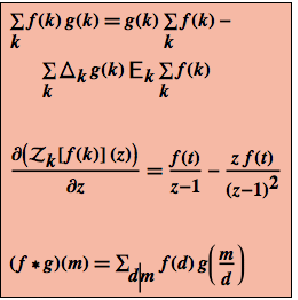Apply Formal Operators in Discrete Calculus
Formal operations can be applied with ease for discrete calculus operations such as differencing, summation, and Z transforms.
Verify that DifferenceDelta is the inverse of Sum.
| In[1]:= | X |
| Out[1]= |
| In[2]:= | X |
| Out[2]= |
Verify that DiscreteRatio is the inverse of Product.
| In[3]:= | X |
| Out[3]= |
| In[4]:= | X |
| Out[4]= |
Apply DifferenceDelta to an indefinite sum.
| In[5]:= | X |
| Out[5]= |
This is significantly faster than the evaluated version.
| In[6]:= | X |
| Out[6]= |
Apply standard properties of ZTransform.
| In[7]:= | X |
| Out[7]= |
| In[8]:= | X |
| Out[8]= |
| In[9]:= | X |
| Out[9]= |