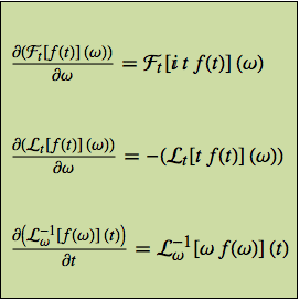Use Feynman's Trick for Evaluating Integrals
Inactive can be used to derive identities by applying standard techniques such as Feynman's trick of differentiating under the integral sign.
Derive a closed form for  by analyzing
by analyzing 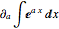 .
.
| In[1]:= | X |
| Out[1]= |
First differentiating with respect to 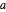 at
at 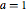 produces the desired integral.
produces the desired integral.
| In[2]:= | X |
| Out[2]= |
If the integration is done first, the integral is simple.
| In[3]:= | X |
| Out[3]= |
The derivative with respect to 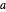 at
at  is also straightforward.
is also straightforward.
| In[4]:= | X |
| Out[4]= |
| In[5]:= | X |
| Out[5]= |
Equating the two expressions produces the answer.
| In[6]:= | X |
| Out[6]//TraditionalForm= | |
Verify the answer.
| In[7]:= | X |
| Out[7]= |