Use Inactive for Debugging a Program
By activating parts of a program in stages, Inactive can assist the debugging process.
The following program contains an error.
| In[1]:= |  X |
Multiple messages are produced, and the integral returns unevaluated.
| In[2]:= | X |
| Out[2]= |
Create an inactive version of the program.
| In[3]:= | X |
| In[4]:= | X |
| Out[4]= |
Everything looks fine, so try activating the function 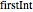 .
.
| In[5]:= | X |
| Out[5]= |
A message is produced, and the inner NIntegrate shows 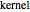 failed to evaluate—it is missing its second argument. Correct the definition.
failed to evaluate—it is missing its second argument. Correct the definition.
| In[6]:= | X |
Now evaluation proceeds correctly.
| In[7]:= | X |
| Out[7]= |
| In[8]:= | X |
| Out[8]= |