Compute Centroids 

The centroid is also known as center of mass for a region and corresponds to a measure of center location for a region. The centroid is given by an integral 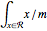, where 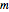is the measure of the region .

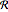Regions in 1D.

In[1]:=

X RegionCentroid[Point[{{0}, {1}, {3}}]]

Out[1]=

In[2]:=

X RegionCentroid[Line[{{0}, {1}, {3}}]]

Out[2]=

Regions in 2D.

In[3]:=

X RegionCentroid[Disk[{x, y}, r]]

Out[3]=

In[4]:=

X RegionCentroid[Rectangle[{xmin, ymin}, {xmax, ymax}]]

Out[4]=

In[5]:=

X RegionCentroid[Polygon[{{0, 0}, {3, -1}, {1, 0}, {3, 1}}]]

Out[5]=

In[6]:=

X RegionCentroid[Polygon[{{0, 0}, {3, -1}, {1, 0}, {3, 1}}]]; Graphics[{LightBlue, Polygon[{{0, 0}, {3, -1}, {1, 0}, {3, 1}}], Red, Point[%]}]

Out[6]=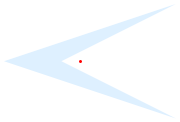

In[7]:=

X \[ScriptCapitalR] = DelaunayMesh[RandomReal[1, {25, 2}]]

Out[7]=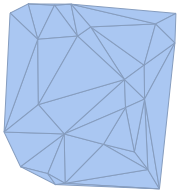

In[8]:=

X Show[\[ScriptCapitalR], Graphics[{Red, PointSize[Medium], Point@RegionCentroid[\[ScriptCapitalR]]}]]

Out[8]=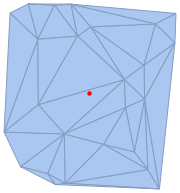

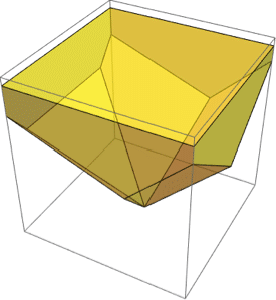
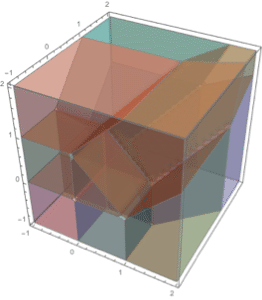
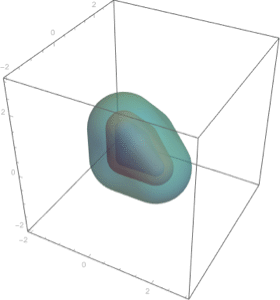
Regions in 3D.

In[9]:=

X RegionCentroid[Ball[{x, y, z}, r]]

Out[9]=

In[10]:=

X RegionCentroid[Tetrahedron[]]

Out[10]=

In[11]:=

X \[ScriptCapitalR] = Polygon[{{0, 0, 0}, {5/3, 2/3, -(4/3)}, {2/3, 2/3, -(1/3)}, {1, 2, 0}}];

In[12]:=

X Graphics3D[{LightBlue, \[ScriptCapitalR], Red, PointSize[Large], Point[RegionCentroid[\[ScriptCapitalR]]]}]

Out[12]=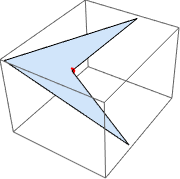

In[13]:=

X \[ScriptCapitalR] = HighlightMesh[ DiscretizeGraphics[ ExampleData[{"Geometry3D", "StanfordBunny"}]], {Style[1, None], Style[2, Opacity[0.5]]}]

Out[13]=

In[14]:=

X RegionCentroid[\[ScriptCapitalR]]

Out[14]=

In[15]:=

X RegionCentroid[\[ScriptCapitalR]]; Show[\[ScriptCapitalR], Graphics3D[{Red, Point[%]}]]

Out[15]=

Regions in D.

In[16]:=

X RegionCentroid[Ball[{x, y, z, w}, r]]

Out[16]=

In[17]:=

X RegionCentroid[Simplex[10]]

Out[17]=