WOLFRAM

New in Mathematica 10 › Symbolic Geometry ›

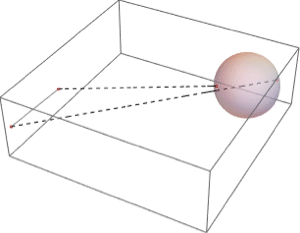
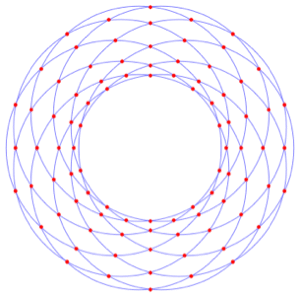
Integrate over Regions 

Integrate over any region. The actual integral used depends on the dimension of the region: a curve integral for one-dimensional integrals, a surface integral for two-dimensional regions, etc. Integrals can be computed symbolically or numerically.

The curve length is an integral over a curve.

In[1]:=
Click for copyable input
X
Out[1]=
In[2]:=
Click for copyable input
X
Out[2]=

The surface area is an integral over a surface.

In[3]:=
Click for copyable input
X
Out[3]=
In[4]:=
Click for copyable input
X
Out[4]=

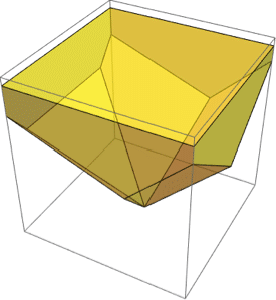
The solid volume is an integral over a solid.

In[5]:=
Click for copyable input
X
Out[5]=
In[6]:=
Click for copyable input
X
Out[6]=

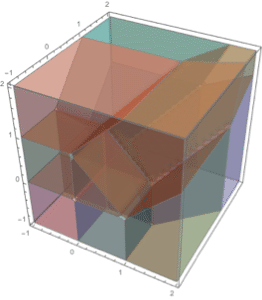
Integrate in any number of dimensions.

In[7]:=
Click for copyable input
X
Out[7]=

Use symbolic vector variables.

In[8]:=
Click for copyable input
X
Out[8]=
In[9]:=
Click for copyable input
X
Out[9]=

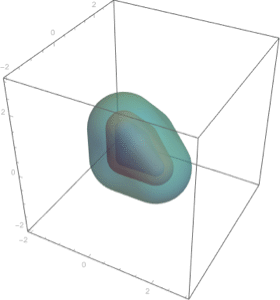
Integrate over any region.

In[10]:=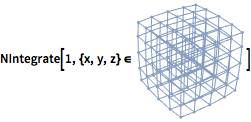
Click for copyable input
X
Out[10]=
In[11]:=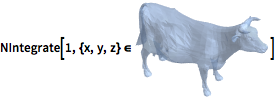
Click for copyable input
X
Out[11]=
In[12]:=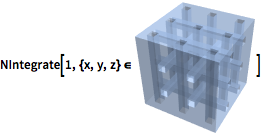
Click for copyable input
X
Out[12]=

Related Examples

Basic Regions » Formula Regions » Mesh Regions » Derived Regions »
Compute Measures (Length, Area, Volume, etc.) » Compute Centroids » Compute Nearest Points » Compute Minimal Distances »
Integrate over Regions » Solve Partial Differential Equations over Regions » Optimize over Regions » Solve Equations over Regions »
de es ja pt-br zh