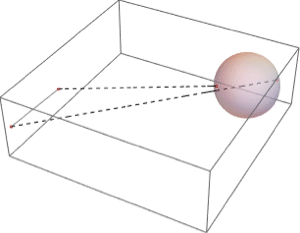
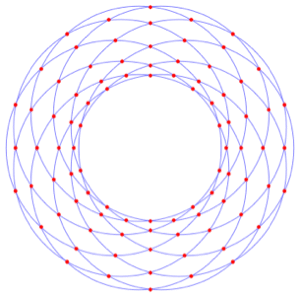
Derived Regions 

Derived regions are regions constructed from other regions. Typical examples include using Boolean combinations of other regions, transformations of other regions, or Cartesian products of regions. Derived regions make it possible to build up a region incrementally in steps. In the Wolfram Language, derived regions can represent regions exactly and approximately.

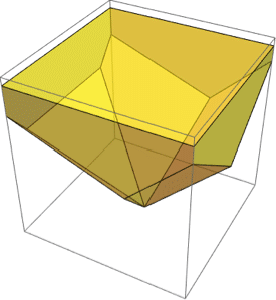
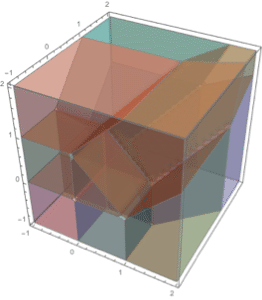
Boolean combinations of regions.

In[1]:=

X r1 = Disk[{-1/2, 0}]; r2 = Disk[{1/2, 0}];

In[2]:=

X d1 = RegionUnion[r1, r2]; d2 = RegionIntersection[r1, r2]; d3 = RegionDifference[r1, r2]; d4 = RegionSymmetricDifference[r1, r2];

In[3]:=

X Table[Show[BoundaryDiscretizeRegion[r], PlotRange -> {{-1.65, 1.65}, {-1.1, 1.1}}, PlotLabel -> Head[r]], {r, {d1, d2, d3, d4}}]

Out[3]=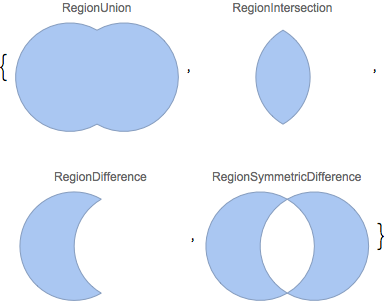

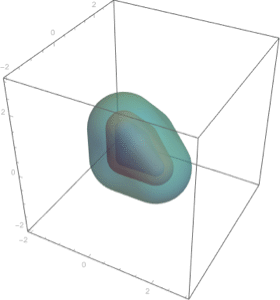
Transformations of regions.

In[4]:=

X r = DiscretizeGraphics[Cuboid[]]

Out[4]=

In[5]:=

X t1 = ScalingTransform[{2, 1, 1}]; t2 = RotationTransform[\[Pi]/3, {1, 1, 1}]; t3 = ShearingTransform[\[Pi]/6, {1, 1, 0}, {0, 0, 1}]; t4 = Composition[t3, t2, t1];

In[6]:=

X Table[TransformedRegion[r, t], {t, {t1, t2, t3, t4}}]

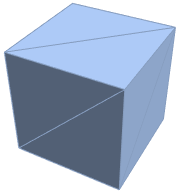Out[6]=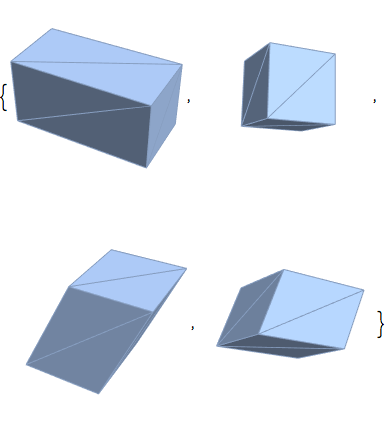

Cartesian product of regions.

In[7]:=

X CantorLine[n_Integer?NonNegative] := Module[{ints, cantor = {a_, b_} :> {{a, a + (b - a)/3}, {a + (b - a) 2/3, b}}}, ints = Nest[ Flatten[Map[Function[s, s /. cantor], #], 1] &, {{0, 1}}, n]; MeshRegion[Transpose[{Flatten[ints]}], Line@Table[{i, i + 1}, {i, 1, Length[ints] 2, 2}]]]

In[8]:=

X Table[CantorLine[k], {k, 0, 3}]

Out[8]=

In[9]:=

X RegionProduct[CantorLine[3], CantorLine[3]]

Out[9]=

In[10]:=

X RegionProduct[CantorLine[3], CantorLine[3], CantorLine[3]]

Out[10]=