Compute Measures (Length, Area, Volume, etc.) 

The measure of a region corresponds to length of a curve, area of a surface, and volume of a solid. But it also generalizes to zero-dimensional objects where the measure is counted, as well as -dimensional objects where the measure is a generalized volume. 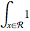For a region containing parts with different dimensions, the measure is taken to be the one that corresponds to the maximal dimension, and the measure is given by the integral , where 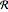is the region.

Curve lengths.

In[1]:=

X ArcLength[Circle[]]

Out[1]=

In[2]:=

X ArcLength[Line[{{0, 0, 0}, {1, 1, 0}, {2, 0, 1}}]]

Out[2]=

In[3]:=

X ArcLength[ImplicitRegion[x^2 + (y/2)^2 == 1, {x, y}]]

Out[3]=

In[4]:=

X ArcLength[Circle[{x, y}, {a, b}], Assumptions -> a > 0 && b > 0]

Out[4]=

In[5]:=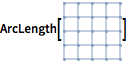

X ArcLength[\!\(\* GraphicsBox[ TagBox[ DynamicModuleBox[{Typeset`mesh = HoldComplete[ MeshRegion[CompressedData[" 1:eJxTTMoPSmViYGCQBGIQDQEf7LHTDA6ofA40vgAaX8QBuz4GB+w0BxpfAI0v gqYO3R3o5qDTAmh8ETRxdH+guwPdHHRaBI3GFQ7o/kB3B8IcACReGVU= "], { Line[{{1, 2}, {1, 6}, {2, 3}, {2, 7}, {3, 4}, {3, 8}, {4, 5}, {4, 9}, {5, 10}, {6, 7}, {6, 11}, {7, 8}, {7, 12}, {8, 9}, {8, 13}, {9, 10}, {9, 14}, {10, 15}, {11, 12}, {11, 16}, {12, 13}, {12, 17}, {13, 14}, {13, 18}, {14, 15}, {14, 19}, {15, 20}, {16, 17}, {16, 21}, {17, 18}, {17, 22}, {18, 19}, {18, 23}, {19, 20}, {19, 24}, {20, 25}, {21, 22}, {22, 23}, {23, 24}, {24, 25}}]}, Method -> {"EliminateUnusedCoordinates" -> True, "DeleteDuplicateCoordinates" -> Automatic, "VertexAlias" -> Identity, "CheckOrientation" -> True, "CoplanarityTolerance" -> Automatic, "CheckIntersections" -> Automatic, "BoundaryNesting" -> Automatic, "SeparateBoundaries" -> False, "PropagateMarkers" -> True, "Hash" -> 8546255060038617691}]]}, TagBox[GraphicsComplexBox[CompressedData[" 1:eJxTTMoPSmViYGCQBGIQDQEf7LHTDA6ofA40vgAaX8QBuz4GB+w0BxpfAI0v gqYO3R3o5qDTAmh8ETRxdH+guwPdHHRaBI3GFQ7o/kB3B8IcACReGVU= "], {Hue[0.6, 0.3, 0.75], LineBox[{{1, 2}, {1, 6}, {2, 3}, {2, 7}, {3, 4}, {3, 8}, {4, 5}, {4, 9}, {5, 10}, {6, 7}, {6, 11}, {7, 8}, {7, 12}, {8, 9}, {8, 13}, {9, 10}, {9, 14}, {10, 15}, {11, 12}, {11, 16}, {12, 13}, {12, 17}, {13, 14}, {13, 18}, {14, 15}, {14, 19}, {15, 20}, {16, 17}, {16, 21}, {17, 18}, {17, 22}, {18, 19}, {18, 23}, {19, 20}, {19, 24}, {20, 25}, {21, 22}, {22, 23}, {23, 24}, {24, 25}}], {PointBox[{{1}}], PointBox[{{2}}], PointBox[{{3}}], PointBox[{{4}}], PointBox[{{5}}], PointBox[{{6}}], PointBox[{{7}}], PointBox[{{8}}], PointBox[{{9}}], PointBox[{{10}}], PointBox[{{11}}], PointBox[{{12}}], PointBox[{{13}}], PointBox[{{14}}], PointBox[{{15}}], PointBox[{{16}}], PointBox[{{17}}], PointBox[{{18}}], PointBox[{{19}}], PointBox[{{20}}], PointBox[{{21}}], PointBox[{{22}}], PointBox[{{23}}], PointBox[{{24}}], PointBox[{{25}}]}}], MouseAppearanceTag["LinkHand"]], AllowKernelInitialization->False], "MeshGraphics", AutoDelete->True, Editable->False, Selectable->False], DefaultBaseStyle->{ "Graphics", FrontEnd`GraphicsHighlightColor -> Hue[0.1, 1, 0.7]}]\)]

Out[5]=

Surface areas.

In[6]:=

X Area[Disk[]]

Out[6]=

In[7]:=

X Area[SSSTriangle[3, 4, 5]]

Out[7]=

In[8]:=

X Area[Polygon[{{0, 0}, {1, 1}, {2, 0}}]]

Out[8]=

In[9]:=

X Area[ImplicitRegion[x^2 + (y/3)^2 <= 1, {x, y}]]

Out[9]=

In[10]:=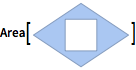

X Area[\!\(\* GraphicsBox[ TagBox[ DynamicModuleBox[{Typeset`mesh = HoldComplete[ BoundaryMeshRegion[{{-3., 0.}, {0., -2.}, {3., 0.}, {0., 2.}, {-1., -1.}, {1., -1.}, {1., 1.}, {-1., 1.}}, { Line[{{1, 2}, {2, 3}, {3, 4}, {4, 1}}]}, { Line[{{5, 6}, {6, 7}, {7, 8}, {8, 5}}]}, Method -> {"EliminateUnusedCoordinates" -> Automatic, "DeleteDuplicateCoordinates" -> Automatic, "VertexAlias" -> Identity, "CheckOrientation" -> True, "CoplanarityTolerance" -> Automatic, "CheckIntersections" -> Automatic, "BoundaryNesting" -> {{0, 0}, {1, 1}}, "SeparateBoundaries" -> False, "Hash" -> 7060032376378194648}]]}, TagBox[GraphicsComplexBox[{{-3., 0.}, {0., -2.}, {3., 0.}, {0., 2.}, {-1., -1.}, {1., -1.}, {1., 1.}, {-1., 1.}}, {Hue[0.6, 0.3, 0.95], EdgeForm[Hue[0.6, 0.3, 0.75]], FilledCurveBox[{{Line[{1, 2, 3, 4}]}, { Line[{5, 6, 7, 8}]}}]}], MouseAppearanceTag["LinkHand"]], AllowKernelInitialization->False], "MeshGraphics", AutoDelete->True, Editable->False, Selectable->False], DefaultBaseStyle->{ "Graphics", FrontEnd`GraphicsHighlightColor -> Hue[0.1, 1, 0.7]}, ImageSize->{100., Automatic}]\)]

Out[10]=

Solid volumes.

In[11]:=

X Volume[Ball[]]

Out[11]=

In[12]:=

X Volume[Tetrahedron[]]

Out[12]=

In[13]:=

X Volume[ImplicitRegion[x^2 + y^2 + (z/3)^2 <= 1, {x, y, z}]]

Out[13]=

In[14]:=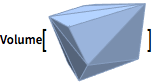

X Volume[\!\(\* Graphics3DBox[ TagBox[ DynamicModuleBox[{Typeset`mesh = HoldComplete[ MeshRegion[CompressedData[" 1:eJwBaQKW/SFib1JlAgAAABkAAAADAAAAYAJai0Yp4j9gQ0x+IerpP2D+vO+2 zqc/TMahkzer2T+Ahi9CwTG2P1ydHUVeFew/sGm9bGIgyj9YopeVD+blPwA3 iXcAebU/QBGwsqoptz90PCPsdLTVP/iibYMyEN8/wBtdfJqFlj/QkxCehfTm P6iJobOS/sg/GOWiFY5a2j9ka9aroG7YPxJAkXrbru8/IGiFkZVZsz+AtJz8 QV3lP8hkeOO2dNg/FI9mVtjK2z/aMEH6hJDpP/h/QXQA88s/EGAN8YLQ2D+g KLFiJofmP+4xlB1JBOs/EorAPqCk5z8Ag98EjXrrP/TYCXhL9uQ/mndnKJcc 5j8+wY/L+bfsPwLR+kGLqOY/HDmVuSU+0j9QvEHsE7rGP2JGXzDpTOw/hD0Q zu3N3z8gUU3WZ8W1P7BO6kLvhsI/TCd52FtW5j+8ee/FvjnaP2T2OhAWt+Q/ 9OwOw+dZ0z9s7F/6prvfP57Cm4OjNew/GJcFJR0axz+gRiyy/JGrP3YQYeES wO4/Tnmut+/77z/gsBnCqYDnP9rKwaTU5+8/WIOhZFK94z+wGakKDq63P/Rs mxYuqts/5KQRe7Xe4T+oJX8YEdPkP9icRExjyNM/ANKgzd8pzz/oVsOi3FLR P9R890jv8OU/QPvWD1x9wz8GYWybUybkP4xYWQcLy+U/6MnQHNcBzD+0twf5 Y5vRP+gUes1ooMU/HNqs2UOy7T86vG6LYZ/tP8Bh5xoCN6E/vI+WCc/03T/A h5D5C+jKP3SZaPtgrec/ACoup8K44D8+OA7S0+XgP+w64eht3NM/rfY3hA== "], { Tetrahedron[CompressedData[" 1:eJwNkDl2BSEMwD67gcEstgGXuVJeTpAL5P5dptBTLX39/n3/2s/n8/PiX1Q8 ayIgc1S3aerMvk/sKXjBOsvFpWtrK3UeKniwzFMLwcLXOQjGmemg4ll6dbFL CiY4QFFGvv3y008wsPS0icsuvHZWzEYJjFN4bBw+6Q7JQTkEIfl9LUa0M9Zw wD6XawpQT4FjCI6a5lLYqQahUnMtmLFQjhl7BcqkmG28j9mu3Yhdk9ua3ha9 nAV7giqQq1BS0UxCkIQyiDB2zCrLXvZbWfdi3zbvtjjaOd4lw0sYD9uxmx+e ZTydB3cZi9uwvEZjP/4B+NYUlQ== "]]}, Method -> {"EliminateUnusedCoordinates" -> True, "DeleteDuplicateCoordinates" -> Automatic, "VertexAlias" -> Identity, "CheckOrientation" -> True, "CoplanarityTolerance" -> Automatic, "CheckIntersections" -> Automatic, "BoundaryNesting" -> Automatic, "SeparateBoundaries" -> False, "PropagateMarkers" -> True, "Hash" -> 3799271606459298466}]]}, TagBox[GraphicsComplex3DBox[CompressedData[" 1:eJwBaQKW/SFib1JlAgAAABkAAAADAAAAYAJai0Yp4j9gQ0x+IerpP2D+vO+2 zqc/TMahkzer2T+Ahi9CwTG2P1ydHUVeFew/sGm9bGIgyj9YopeVD+blPwA3 iXcAebU/QBGwsqoptz90PCPsdLTVP/iibYMyEN8/wBtdfJqFlj/QkxCehfTm P6iJobOS/sg/GOWiFY5a2j9ka9aroG7YPxJAkXrbru8/IGiFkZVZsz+AtJz8 QV3lP8hkeOO2dNg/FI9mVtjK2z/aMEH6hJDpP/h/QXQA88s/EGAN8YLQ2D+g KLFiJofmP+4xlB1JBOs/EorAPqCk5z8Ag98EjXrrP/TYCXhL9uQ/mndnKJcc 5j8+wY/L+bfsPwLR+kGLqOY/HDmVuSU+0j9QvEHsE7rGP2JGXzDpTOw/hD0Q zu3N3z8gUU3WZ8W1P7BO6kLvhsI/TCd52FtW5j+8ee/FvjnaP2T2OhAWt+Q/ 9OwOw+dZ0z9s7F/6prvfP57Cm4OjNew/GJcFJR0axz+gRiyy/JGrP3YQYeES wO4/Tnmut+/77z/gsBnCqYDnP9rKwaTU5+8/WIOhZFK94z+wGakKDq63P/Rs mxYuqts/5KQRe7Xe4T+oJX8YEdPkP9icRExjyNM/ANKgzd8pzz/oVsOi3FLR P9R890jv8OU/QPvWD1x9wz8GYWybUybkP4xYWQcLy+U/6MnQHNcBzD+0twf5 Y5vRP+gUes1ooMU/HNqs2UOy7T86vG6LYZ/tP8Bh5xoCN6E/vI+WCc/03T/A h5D5C+jKP3SZaPtgrec/ACoup8K44D8+OA7S0+XgP+w64eht3NM/rfY3hA== "], {Hue[0.6, 0.3, 0.85], EdgeForm[Hue[0.6, 0.3, 0.75]], TetrahedronBox[CompressedData[" 1:eJwNkDl2BSEMwD67gcEstgGXuVJeTpAL5P5dptBTLX39/n3/2s/n8/PiX1Q8 ayIgc1S3aerMvk/sKXjBOsvFpWtrK3UeKniwzFMLwcLXOQjGmemg4ll6dbFL CiY4QFFGvv3y008wsPS0icsuvHZWzEYJjFN4bBw+6Q7JQTkEIfl9LUa0M9Zw wD6XawpQT4FjCI6a5lLYqQahUnMtmLFQjhl7BcqkmG28j9mu3Yhdk9ua3ha9 nAV7giqQq1BS0UxCkIQyiDB2zCrLXvZbWfdi3zbvtjjaOd4lw0sYD9uxmx+e ZTydB3cZi9uwvEZjP/4B+NYUlQ== "]]}], MouseAppearanceTag["LinkHand"]], AllowKernelInitialization->False], "MeshGraphics", AutoDelete->True, Editable->False, Selectable->False], Boxed->False, DefaultBaseStyle->{ "Graphics3D", FrontEnd`GraphicsHighlightColor -> Hue[0.1, 1, 0.7]}, ImageSize->{100.21877533737324`, Automatic}, Lighting->{{"Ambient", GrayLevel[0.45]}, {"Directional", GrayLevel[0.3], ImageScaled[{2, 0, 2}]}, {"Directional", GrayLevel[0.33], ImageScaled[{2, 2, 2}]}, {"Directional", GrayLevel[0.3], ImageScaled[{0, 2, 2}]}}, Method->{"ShrinkWrap" -> True}, ViewPoint->{1.309914677685133, -2.41828679120594, 1.9712971700542594`}, ViewVertical->{0.007619178700136017, -0.008734435802095196, 1.014557463829864}]\)]

Out[14]=

General -dimensional measures for unit spheres, balls, and simplices.

In[15]:=

X Table[RegionMeasure[Sphere[n]], {n, 1, 10}]

Out[15]=

In[16]:=

X Table[RegionMeasure[Sphere[n]], {n, 1, 10}]; FindSequenceFunction[%, n] // FullSimplify

Out[16]=

In[17]:=

X Table[RegionMeasure[Ball[n]], {n, 1, 10}]

Out[17]=

In[18]:=

X Table[RegionMeasure[Ball[n]], {n, 1, 10}]; FindSequenceFunction[%, n] // FullSimplify

Out[18]=

In[19]:=

X Table[RegionMeasure[Simplex[n]], {n, 1, 10}]

Out[19]=

In[20]:=

X Table[RegionMeasure[Simplex[n]], {n, 1, 10}]; FindSequenceFunction[%, n] // FullSimplify

Out[20]=