クロマトグラフィーカラム
クロマトグラフィーは化合物の解析および浄化の両方にとって最も重要なツールの一つです.クロマトグラフィーカラムにはさまざまな大きさがありますが,基本的な原理はどれも同じです.さまざまな分子間相互作用によって,さまざまな物質がさまざまな速度でカラム内を流れ,事実上互いから分離します.このモデルはそのような相互作用を調べます.この例を実行するためには,ここからダウンロードできる無料のBioChem Modelicaライブラリが必要です.
モデル
クロマトグラフィーカラムは移動相と固定相の2つの相で説明することができます.物質は平衡状態にある2つの相の間を移動します.移動相の物質はカラムの下にも向かって移動します.カラムの各点における2つの相の物質の濃度は偏微分方程式で表せます.線の方法を使うと,空間点が離散化でき結果の微分代数方程式を数値的に解くことができます.

モデルの偏微分方程式はMathematicaで離散化され,自動的にModelicaコードに変換される.
コードの自動生成
MathematicaはSystem Modelerで直接シミュレーションを実行することができるModelicaコードを生成し,エキスポートすることができます.
この例では無料のModelicaライブラリBioChemを使ってモデル化された簡単な生化学反応を解析するために,クロマトグラフィーカラムが使われています.分光光度計を使ってカラムの溶離液を継続的に監視すると,特定の物質の溶出を示す顕著なピークが見られます.システムのシミュレーションを行うと,それぞれの物質がプロファイルにどのように関係しているかを見るために溶出プロファイルを解析することができます.
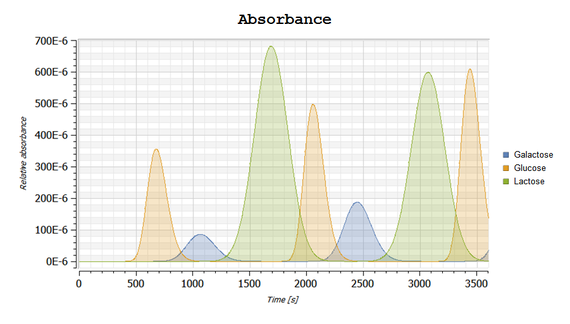
各物質がどのように溶出プロファイルに関係しているかを示すプロット
システムとのインタラクション
シミュレーション結果をMathematicaにインポートすると,クロマトグラフィーカラムの内部を可視化することができます.計算可能ドキュメント形式(CDF)を使ってインタラクティブな可視化を配備したり配布したりすることができます.
カラム内部における物質分離と,各物質が分光光度計からの出力信号にどのように関係しているかを表現したもの
結果とインタラクトする
SystemModelerからの結果は,Mathematicaにインポートして,さらに解析を実行することができます.
Wolfram System Modeler
評価版
ご購入
System ModelerはWindows,macOS,
Linuxで
日本語と英語でご利用になれます »
ご質問やコメントはWolframエキスパートまでお寄せください »