Complex Analysis
The imaginary unit ![]() is represented as I:
is represented as I:
| In[1]:= |
| Out[1]= |
Most operations automatically handle complex numbers:
| In[2]:= |
| Out[2]= |
Expand complex expressions:
| In[1]:= |
| Out[1]= |
Convert expressions between exponential and trig forms:
| In[2]:= |
| Out[2]= |
| In[3]:= |
| Out[3]= |
Type ESCcoESC for the Conjugate symbol:
| In[1]:= |
| Out[1]= |
Extract the real and imaginary parts of an expression:
| In[2]:= |
| Out[2]= |
Or find the absolute value and argument:
| In[3]:= |
| Out[3]= |
Plot a conformal mapping with ParametricPlot:
| In[1]:= |
| Out[1]= | 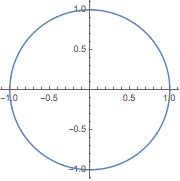 |
| In[2]:= |
| Out[2]= | 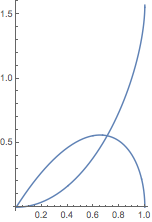 |
Visualize complex components with a DensityPlot:
| In[3]:= |
| Out[3]= | 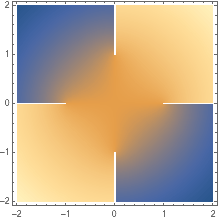 |
QUICK REFERENCE: Complex Numbers »
QUICK REFERENCE: Functions of Complex Variables »
