Symmetric Matrices
Undirected graphs must have symmetric adjacency matrices.
| In[1]:= | X |
| In[2]:= | X |
| Out[2]= | 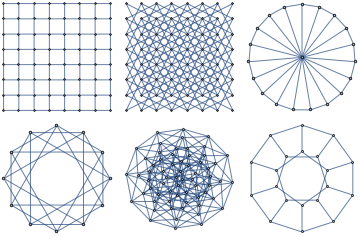 |
Verify the symmetry.
| In[3]:= | X |
| Out[3]= |
Directed graphs typically have non-symmetric adjacency matrices.
| In[4]:= |  X |
| In[5]:= |  X |
| Out[5]= | 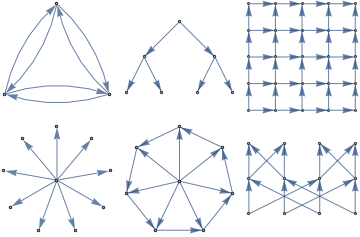 |
In the above examples, the complete graph has a symmetric adjacency matrix, but all the other graphs have a non-symmetric adjacency matrix.
| In[6]:= | X |
| Out[6]= |
Visualize the adjacency matrices for both directed and undirected graphs.
| In[7]:= |  X |
| Out[7]= |  |