Model the Conditional Value at Risk with an ARCHProcess
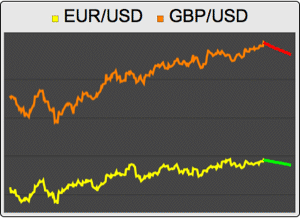
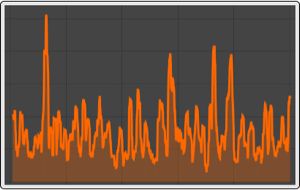
The returns of Apple stock from January 2009 to April 2014.
| In[2]:= | X |
| In[3]:= | X |
| Out[3]= |  |
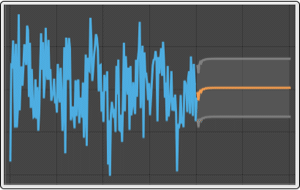
Split the time series in two parts, and use the first part to find a model.
| In[4]:= | X |
| Out[4]= |
| In[5]:= | X |
| Out[5]= |
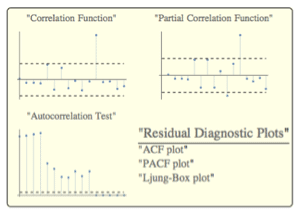
Fit an ARCHProcess to the first time series.
| In[6]:= | X |
| Out[6]= | 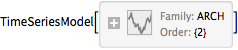 |
| In[7]:= | X |
| Out[7]= |
| In[8]:= | X |
| Out[8]= |
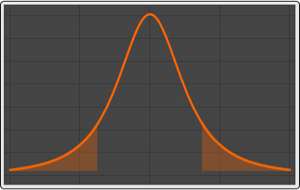
Find the conditional value at risk for the second part of the time series with significance level at 95%.
| In[9]:= |  X |
| Out[9]= |
Plot the second time series and its values at risk.
| In[10]:= | X |
| Out[10]= | 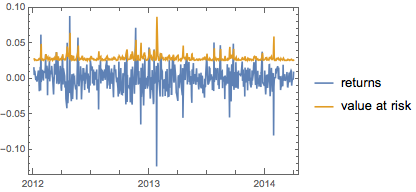 |