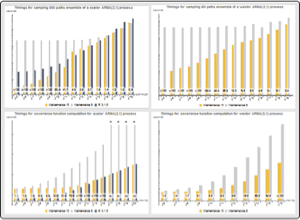
Study Non-weakly Stationary Autoregressive Process 

Mathematica 10 supports time series processes with given past values, which cover both the stationary time series conditioned on past values as well as nonstationary time series with initial conditions. When autoregressive coefficients do not satisfy the stationarity condition, variance function of the time process slice grows unboundedly.

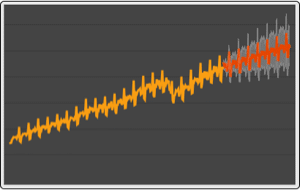
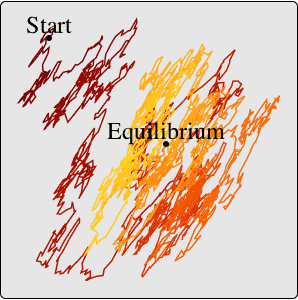
Define an autoregressive process whose autoregressive coefficients do not satisfy the weak stationarity condition.

In[1]:=

X cond = WeakStationarity[ARProcess[{a1, a2}, var]]

Out[1]=

In[2]:=

X cond /. {a1 -> -1/2, a2 -> 1/2}

Out[2]=

In[3]:=

X arProc = ARProcess[{-1/2, 1/2}, 1, {}];

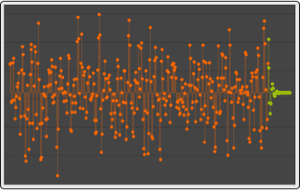
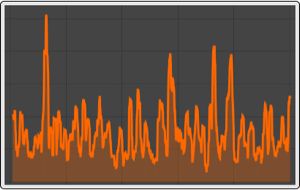
Sample the process.

In[4]:=

X path = RandomFunction[arProc, {0, 500}];

In[5]:=

X ListPlot[path, Filling -> Axis]

Out[5]=

Compute the mean function and the covariance function of the process.

In[6]:=

X Mean[arProc[t]]

Out[6]=

In[7]:=

X covF = Refine[ CovarianceFunction[arProc, s, s + h], {s, h} \[Element] Integers && s >= 0 && h >= 0]

Out[7]=

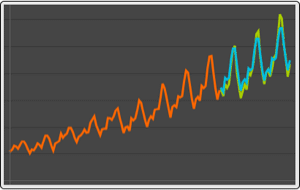
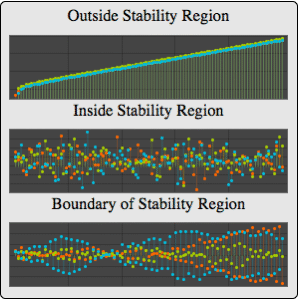
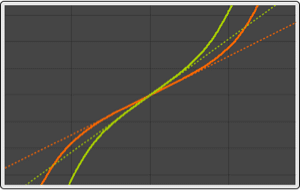
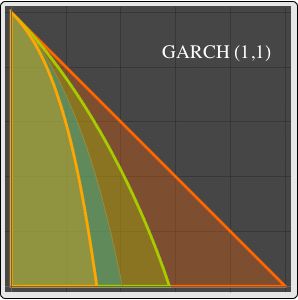
Visualize the covariance function as a function of time 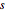for a few values of the lag .

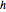In[8]:=

X Table[DiscretePlot[covF, {s, 0, 6}, ExtentSize -> Full, AxesOrigin -> {-1, 0}, ExtentElementFunction -> "ArrowRectangle", ColorFunction -> "Rainbow", AxesLabel -> {s, Cov[x[s], x[s + h]]}], {h, 0, 3}] // Partition[#, 2] & // Grid

Out[8]=