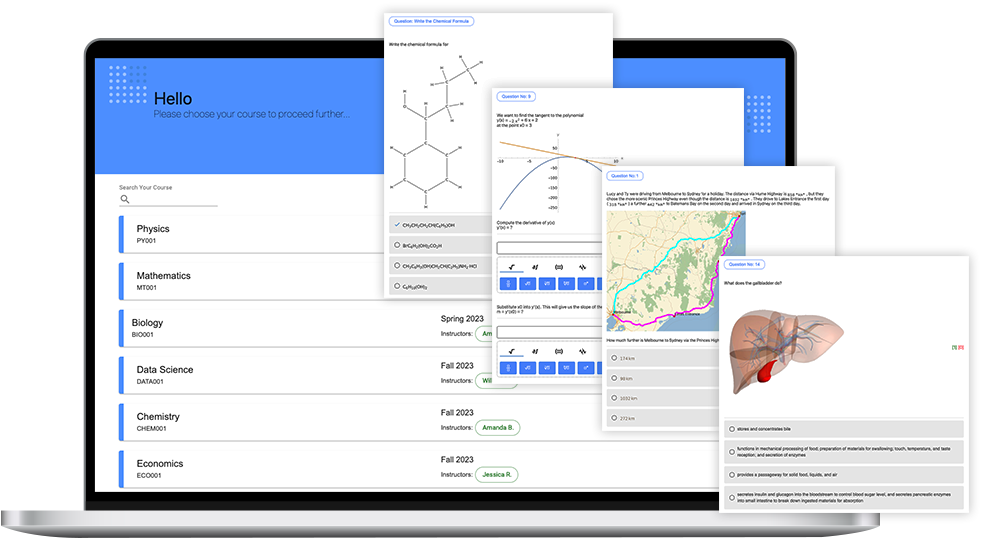
Was ist Quezzio?
Quezzio ist eine Plattform, die genutzt werden kann, um Lernzielevaluierungsfragen über das Lehrbuchmaterial hinaus zu erweitern, durch eingebettete Abbildungen und mathematische Formeln ansprechendere Inhalte zu erstellen und eine präzise Benotung für alle Arten von Beurteilungen anzubieten.
Wer sollte Quezzio nutzen?
Bildungseinrichtungen, die das Erstellen, Verwalten und Bereitstellen von Materialien verbessern möchten
Quezzio bietet erweiterte mathematische Funktionen, rechnerische Unterstützung für Lehrkräfte und kuratierte Daten aus der echten Welt für Beurteilungen.
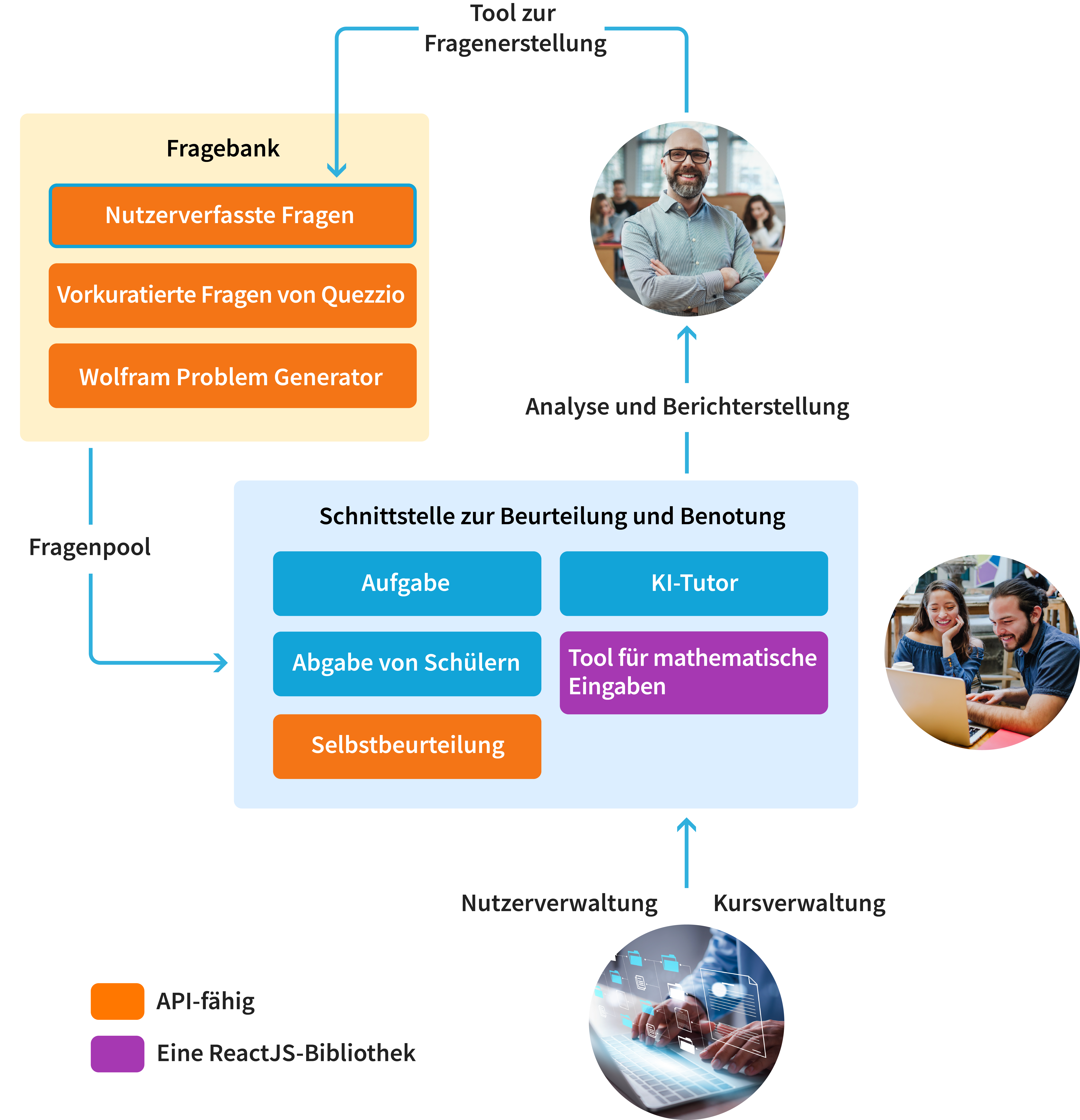
Was ist in Quezzio enthalten?
Die Plattform umfasst sieben Tools, die nahtlos miteinander kombiniert oder als Einzelkomponenten lizenziert werden können.
- Werkzeug zur Fragenerstellung
- Fragenbank
- Kursverwaltungssystem (CMS)/
Lernverwaltungssystem (LMS)
- Schnittstelle zur Schülerbeurteilung
- System zur automatischen Benotung
- Mathematisches Eingabetool
- Analysen und Berichte
Fragenbank und Tool zur Fragenerstellung
Wolfram Problem Generator und zusätzliche vorformulierte Fragen
Der Wolfram Problem Generator bietet eine unbegrenzte Anzahl von KI-generierten Übungsaufgaben und Antworten für die reine Mathematik. Darüber hinaus wird die Fragebank durch eine Bibliothek mit Tausenden von Textaufgaben und visuellen Mathematikaufgaben für die Schulstufen 4 bis 12 ergänzt, die sich an den US-amerikanischen Common Core-Bildungsstandards orientieren. Jede Frage dient als Vorlage für den Austausch von zufälligen Koeffizienten oder Funktionen und bietet so einen sehr großen Pool für verschiedene Variationen von Fragen.
Vorlage-Notebook für Fragen
Verwenden Sie nahtlos verfügbare reale Daten, um neue Fragen zu erstellen und um Grafiken für jedes MINT-Fach einzubetten. Verfügbar für die Fächer Chemie, Physik, Geowissenschaften, Wirtschaft und Finanzwesen.
Integriert in Ihr bestehendes CMS oder als eigenständiges CMS

Fragebank
Nachdem die Fragen erstellt wurden, werden sie in eine Fragebank hochgeladen. Die Fragen können dann für Hausaufgaben, Tests und andere Kursmaterialien verwendet werden. Sie können auch mit Tags versehen werden, damit sie bei der Verwaltung einer großen Fragenbank in verschiedenen Kursen und Disziplinen leichter zu finden sind.
Nahtlose Integration mit bestehenden CMS-Programmen
Quezzio kann als eigenständiges CMS fungieren oder mit einem bestehenden CMS wie Canvas, Blackboard, D2L oder Moodle verknüpft werden. Bewertungen und Fälligkeitstermine können für bestimmte Kurse und Teilnehmerlisten erstellt werden.

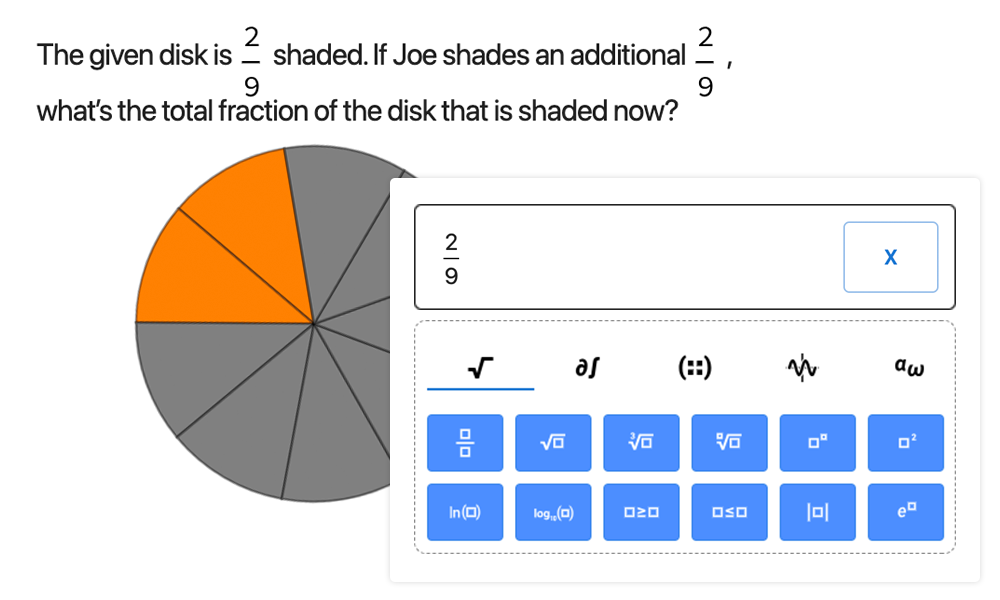
Schnittstelle zur Beurteilung von Schülerinnen und Schülern und zu mathemtischen Eingabetools
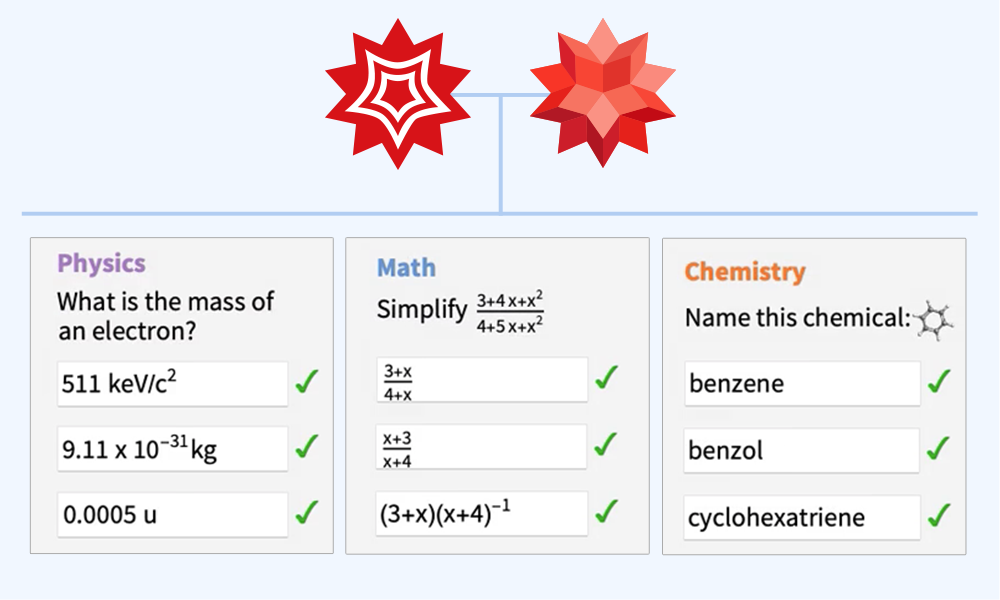
Eine vollständig webbasierte Schnittstelle bietet den Schülern eine Plattform für die Erledigung von Hausaufgaben oder Abfragen. Die Antworten können einfach in Form von mathematischen Ausdrücken eingegeben werden, um Verwechslungen oder Mehrdeutigkeiten zu vermeiden.
Dahinter steckt derselbe Motor zur automatischen Benotung wie bei Wolfram Mathematica und Wolfram|Alpha
Quezzio bietet eine genaue und zuverlässige automatische Beurteilung von Schülerantworten, da es dieselbe Kerntechnologie nutzt, auf die auch die führenden Computerprodukte wie Wolfram|Alpha und Mathematica aufbauen.
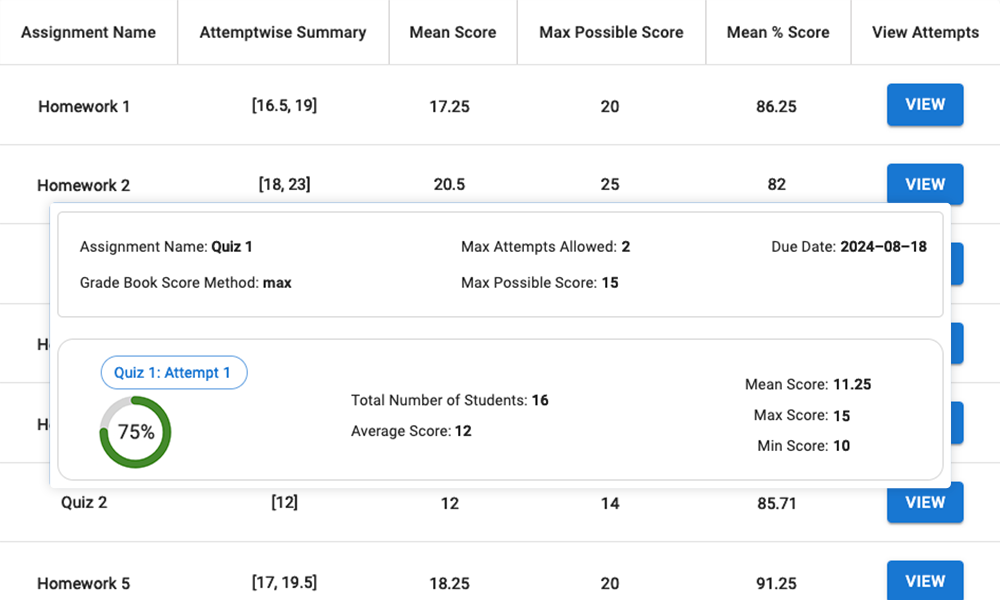
Berichterstellung für Lehrkräfte
Lehrkräfte können genau sehen, was die Schüler am Lösungsweg und als Antworten eingegeben haben, sowie Zusammenfassungen für jeden Schüler oder jede Aufgabe, und die Ergebnisse können in ein externes CMS-Notenbuch (wie Canvas) exportiert werden.
Häufig gestellte Fragen
- F: Ist Quezzio kompatibel mit unserem Loginsystem (LTI, etc.) für Schüler und Schülerinnen? A: Ja. Wir können eine Verknüpfung zu Ihrem Authentifizierungssystem herstellen, um Klassenlisten für bestimmte Kurse automatisch auszufüllen.
- F: Bietet Wolfram Schulungen an, wie man richtig Fragen verfasst? A: Ja. Wolfram bietet personalisierte Schulungen zur Nutzung von Quezzio sowie Beratungsdienste zur Entwicklung und Implementierung maßgeschneiderter Anpassungen der Plattform an Ihre Anforderungen.
- F: Wird das System von Wolfram gehostet, oder können wir das System auf dem Campus hosten? A: Beides ist möglich. Die Plattform kann auf einem Server vor Ort, bei einem Cloud-Anbieter oder auf den Servern von Wolfram laufen.
- F: Setzt das System voraus, dass die Schüler und Schüerinnen Mathematica verwenden oder in der Wolfram Language programmieren können? A: Nein. Das Tool zum Verfassen von Fragen wird in Mathematica ausgeführt, aber die Studierenden sehen keinen Wolfram Language-Code, wenn sie zugewiesene Hausaufgaben oder Testfragen erledigen. Wenn der Kursinhalt auf die Vermittlung von Mathematica und Wolfram Language ausgerichtet ist, können die Antworten der Studenten in Form von Wolfram Language erfolgen und automatisch benotet werden.
- F: Wie verhält sich dies im Vergleich zum Wolfram Problem Generator? A: Der Wolfram Problem Generator ist für anonyme Übungsfragen gedacht, während Quezzio eine Möglichkeit ist, diese Art von Technologie in Ihre Kurse und Benotungssysteme zu integrieren.
- F: Ersetzt Quezzio ein LMS oder CMS wie Canvas? A: Die Plattform kann als eigenständiges CMS fungieren oder mit einem CMS wie Canvas verbunden werden, um Bewertungen zu liefern und in das CMS-Notenbuch zu schreiben.